
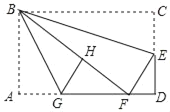
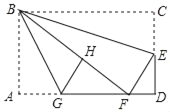
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②S△ABG=![]() S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
【答案】①②④.
【解析】
利用折叠性质得∠CBE=∠FBE,∠ABG=∠FBG,BF=BC=10,BH=BA=6,AG=GH,则可得到∠EBG=![]() ∠ABC,于是可对①进行判断;在Rt△ABF中利用勾股定理计算出AF=8,则DF=AD-AF=2,设AG=x,则GH=x,GF=8-x,HF=BF-BH=4,利用勾股定理得到x2+42=(8-x)2,解得x=3,所以AG=3,GF=5,于是可对②④进行判断;接着证明△ABF∽△DFE,利用相似比得到
∠ABC,于是可对①进行判断;在Rt△ABF中利用勾股定理计算出AF=8,则DF=AD-AF=2,设AG=x,则GH=x,GF=8-x,HF=BF-BH=4,利用勾股定理得到x2+42=(8-x)2,解得x=3,所以AG=3,GF=5,于是可对②④进行判断;接着证明△ABF∽△DFE,利用相似比得到![]() ,而
,而![]() ,所以
,所以![]() ,所以△DEF与△ABG不相似,于是可对③进行判断.
,所以△DEF与△ABG不相似,于是可对③进行判断.
解:∵△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,
将△ABG沿BG折叠,点A恰落在线段BF上的点H处,
∴∠CBE=∠FBE,∠ABG=∠FBG,BF=BC=10,BH=BA=6,AG=GH,
∴∠EBG=∠EBF+∠FBG=![]() ∠CBF+
∠CBF+![]() ∠ABF=
∠ABF=![]() ∠ABC=45°,所以①正确;
∠ABC=45°,所以①正确;
在Rt△ABF中,AF=![]() =
=![]() =8,
=8,
∴DF=AD﹣AF=10﹣8=2,
设AG=x,则GH=x,GF=8﹣x,HF=BF﹣BH=10﹣6=4,
在Rt△GFH中,
∵GH2+HF2=GF2,
∴x2+42=(8﹣x)2,解得x=3,
∴GF=5,
∴AG+DF=FG=5,所以④正确;
∵△BCE沿BE折叠,点C恰落在边AD上的点F处,
∴∠BFE=∠C=90°,
∴∠EFD+∠AFB=90°,
而∠AFB+∠ABF=90°,
∴∠ABF=∠EFD,
∴△ABF∽△DFE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
而![]() =
=![]() =2,
=2,
∴![]() ≠
≠![]() ,
,
∴△DEF与△ABG不相似;所以③错误.
∵S△ABG=![]() ×6×3=9,S△GHF=
×6×3=9,S△GHF=![]() ×3×4=6,
×3×4=6,
∴S△ABG=![]() S△FGH,所以②正确.
S△FGH,所以②正确.
故答案是:①②④.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
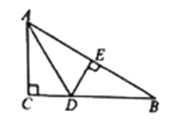
【题目】如图,在△ABC,∠C=90°,AD平分∠BAC交CB于点D,过点D作DE⊥AB,垂足恰好是边AB的中点E.若AD=3cm,则BE的长为( )
A. ![]() cmB. 4cmC. 3
cmB. 4cmC. 3![]() cmD. 6cm
cmD. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了准备“欢乐颂——创意市场”,初2020级某同学到批发市场购买了![]() 、
、![]() 两种原材料,
两种原材料,![]() 的单价为每件6元,
的单价为每件6元,![]() 的单价为每件3元.该同学的创意作品需要
的单价为每件3元.该同学的创意作品需要![]() 材料的数量是
材料的数量是![]() 材料数量的2倍,同时,为了减少成本,该同学购买原材料的总费用不超过480元.
材料数量的2倍,同时,为了减少成本,该同学购买原材料的总费用不超过480元.
(1)该同学最多购买多少件![]() 材料;
材料;
(2)在该同学购买![]() 材料最多的前提下,用所购买的
材料最多的前提下,用所购买的![]() ,
,![]() 两种材料全部制作作品,在制作中其他费用共花了520元,活动当天,该同学在成本价(购买材料费用+其他费用)的基础上整体提高
两种材料全部制作作品,在制作中其他费用共花了520元,活动当天,该同学在成本价(购买材料费用+其他费用)的基础上整体提高![]() 标价,但无人问津,于是该同学在标价的基础上降低
标价,但无人问津,于是该同学在标价的基础上降低![]() 出售,最终,在活动结束时作品卖完,这样,该同学在本次活动中赚了
出售,最终,在活动结束时作品卖完,这样,该同学在本次活动中赚了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
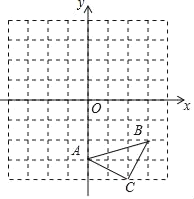
【题目】如图,△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),在正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移4个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C,使△A2B2C与△ABC位似,且△A2B2C与△ABC的位似比为2:1,并直接写出点B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
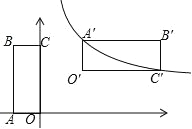
【题目】如图,在平面直角坐标系中,矩形 OABC 的边 OA 与 x 轴重合,B 的坐标为(﹣1,2),将矩形 OABC 绕平面内一点 P 顺时针旋转 90°,使 A、C 两点恰好落在反比例函数 y=![]() 的图象上,则旋转中心 P 点的坐标是( )
的图象上,则旋转中心 P 点的坐标是( )
A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
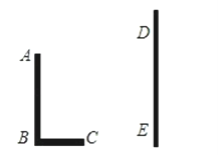
【题目】已知,如图,AB和DE是直立在地面上的两根立柱.AB=7m,某一时刻AB在太阳光下的投影BC=4m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,计算DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com