
����Ŀ��ʵ����̽��
(1)��ͼ�٣�ͼ�ڣ�ͼ���У�����ƽ���ı���ABCD�Ķ���A��B��D�����꣬д��ͼ�٣�ͼ�ڣ�ͼ���еĶ���C�����꣬���Ƿֱ���________��___________��____________��
(2)��ͼ���У�����ƽ���ı���ABCD�Ķ���A��B��D������(��ͼ��ʾ)���������C������(C�������ú�a��b��c��d��e��f�Ĵ���ʽ��ʾ)��
�����뷢��
(3)ͨ����ͼ�٣�ͼ�ڣ�ͼ�ۣ�ͼ�ܵĹ۲�Ͷ���C�������̽������ᷢ�֣�����ƽ���ı���ABCD����ֱ������ϵ���ĸ�λ�ã����䶥��C����Ϊ(m��n)(��ͼ��)ʱ�����ĸ�����ĺ�����a��c��m��e֮��ĵ�����ϵΪ___________��������b��d��n��f֮��ĵ�����ϵΪ__________��(����֤��)
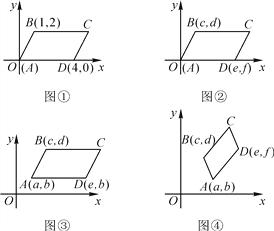
���𰸡�(1) (5��2)��(e��c��d)��(c��e��a��d) ��(2) C(e��c��a��f��d��b) ��(3) m��a��c��e��n��b��d��f
�������������������1������ƽ���ı��ε����ʣ��Ա�ƽ������ȣ��ó�ͼ2��3�ж���C������ֱ��ǣ�e+c��d������c+e��a��d����
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA1��B1��C1��D1���ֱ��A��D��AE��BB1��E��DF��CC1�ڵ�F����ƽ���ı���ABCD�У�CD=BA�������ڽǺͶ���������BB1��CC1�����Ƴ���EBA=��FCD����BEA�ա�CFD��������ó�AF=DF=a��c��BE=CF=d��b����C��x��y������e��x=a��c����x=e+c��a����y��f=d��b����y=f+d��b���̶��Ƴ���C�����꣮
��3����ƽ���ı���ABCD�У�CD=BA��ͬ��֤����BEA�ա�CFD��ͬ��2��֤������Ȼ���Ƴ�AF=DF=a��c��BE=CF=d��b������֪C�������Ϊ��m��n����e��m=a��c����m=e+c��a����n��f=d��b���ó�n=f+d��b��
����������⣺��1������ƽ���ı��ε����ʣ��Ա�ƽ������ȣ��ó�ͼ1��ͼ2��3�ж���C������ֱ��ǣ���5��2������e+c��d������c+e��a��d����
�ʴ�Ϊ����5��2������e+c��d������c+e��a��d����
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA1��B1��C1��D1���ֱ��A��D��AE��BB1��E��DF��CC1�ڵ�F��
��ƽ���ı���ABCD�У�CD=BA������BB1��CC1�����EBA+��ABC+��BCF=��ABC+��BCF+��FCD=180�ȣ����EBA=��FCD��
����BEA����CFD�У��ߡ�AEB=��DFC����EFA=��FCD��AB=DC�����BEA�ա�CFD��AAS������AE=DF=a��c��BE=CF=d��b��
��C��x��y������e��x=a��c������x=e+c��a��
��y��f=d��b������y=f+d��b����C��e+c��a��f+d��b����
��3����ƽ���ı���ABCD�У�CD=BA��ͬ���ɵ���BEA�ա�CFD����AF=DF=a��c��BE=CF=d��b����C�������Ϊ��m��n����e��m=a��c����m=e+c��a����n��f=d��b������n=f+d��b���ʴ�Ϊ��m=c+e��a��n=d+f��b��m+a=c+e��n+b=d+f��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ԭ�ƻ�����24000̨��������������������������Ӱ�죬���������������������������ƣ��������������������12000̨��������ʵ�������У����������Ч�ʣ�ÿ���ԭ�ƻ�������100̨��ʵ��������������������ԭ�ƻ�������1.2������ԭ�ƻ�ÿ����������̨������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڵ����㳡��������ý���ע����������Ƶ��Ϊ�˽��й�ר�ñ�����Сƽ���˽ⱾС����������㳡�����Ŀ�����������һ�γ������飬�Ѿ�������㳡�����Ŀ�����Ϊ�ĸ���Σ�A �dz���ͬ��B ��ͬ��Ҫ��ʱ�����ƣ�C ����ν��D ����ͬ������������������ͼ1��ͼ2������������ͳ��ͼ��

�������ͼ���ṩ����Ϣ����������⣺
��1���α����ľ����ж����ˣ�
��2����ͼ1��ͼ2����������
��3����ͼ2����C������������ε�Բ�ĽǵĶ�����
��4�����Ƹ�С��4000�������ж����㳡�����Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O���ң��뾶OA=2��OA��AB�ij����ǹ���x��һԪ���η���x2��4x+a=0������ʵ������
��1������AB�ij��ȣ�
��2������S��AOB��
��3����O��һ����P��A�����������ʱ�뷽���˶�һ�ܣ���S��POA=S��AOBʱ����P���������Ļ����������ǵ�P���B�غϵ����Σ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.��������������������
B.���������෴�����ǷǸ�����
C.�������в��Ǹ�����������
D.������Ȼ����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ֲij����ɫ�߲ˣ�ȫ���������ڣ�Ϊ��������ڹ�ģ�����о����������߲˵���ֲʵ�������������涨ÿ��ֲ-Ķ�����߲�һ���Բ�����ũ����Ԫ�������飬��ֲĶ��y��Ķ���벹������x��Ԫ��֮�����������ͼ1��ʾ��һ�κ�����ϵ�����Ų�������x�IJ�����������Ҳ�������ӣ���ÿĶ�߲˵�����z��Ԫ������Ӧ���ͣ���z��x֮��Ҳ����������ͼ2��ʾ��һ�κ�����ϵ��
��1��������δ��̨������ʩǰ��������ֲ�����߲˵��������Ϊ���٣�
��2���ֱ����������������ʵʩ����ֲĶ��y��ÿĶ�߲˵�����z��������������x֮��ĺ�����ϵʽ��
��3��Ҫʹȫ�������߲˵�������w��Ԫ���������Ӧ��ÿĶ��������x��Ϊ���٣������������w�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���C(-4��0)����![]() �ֱ���
�ֱ���![]() �ᣬ
�ᣬ ![]() ����������ϣ��߶�OA��OB�ij��ȶ��Ƿ���
����������ϣ��߶�OA��OB�ij��ȶ��Ƿ���![]() .�Ľ⣬��OB��OA������
.�Ľ⣬��OB��OA������![]() ��
��![]() ���������ÿ��1����λ���ٶ�������
���������ÿ��1����λ���ٶ�������![]() �˶�������
�˶�������![]() ��
��
��1���ж�������ABC����״
��2�����![]() �����
�����![]() ���ڵ�
���ڵ�![]() ���˶�ʱ��
���˶�ʱ��![]() ��ĺ�����ϵʽ��
��ĺ�����ϵʽ��
��3���ڵ�P���˶������У����ñ���ͼ̽������![]() �ܳ����ʱ��P�˶���ʱ�䡣
�ܳ����ʱ��P�˶���ʱ�䡣

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com