
分析 设乙工程队每天能完成绿化的面积是xm2,根据在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,列出分式方程,解方程即可.
解答 解:设乙工程队每天能完成绿化的面积是xm2,
根据题意得$\frac{400}{x}$-$\frac{400}{2x}$=4,
解得:x=50.
经检验:x=50是原方程的解.
所以甲工程队每天能完成绿化的面积是50×2=100(m2).
答:甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2.
点评 本题主要考查了分式方程的应用,解题的关键是分析题意,找到合适的数量关系列出分式方程,解分式方程时要注意检验未知数的值是否符合原方程,是否符合实际意义.


科目:初中数学 来源: 题型:解答题
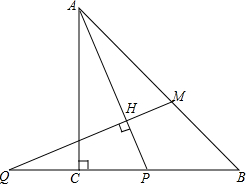 在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
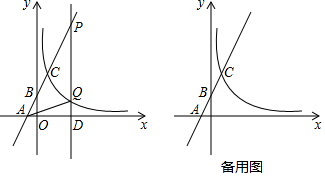
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同圆或等圆中,等现所对的圆周角相等 | |
| B. | 圆的切线垂直于半径 | |
| C. | 三角形的内心是三角形角平分线的交点 | |
| D. | 平分弦的直径垂直于弦 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com