
����Ŀ����ͼ����֪A��B�������ϵ������㣬��A��ʾ����Ϊ13����B��ʾ����Ϊ![]() ������P�ӵ�B��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
������P�ӵ�B��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
(1)��P��ʾ����Ϊ__________���ú�t�Ĵ���ʽ��ʾ����
(2)��P�˶�������ʱ��PB=2PA��
(3)��MΪBP���е㣬NΪPA���е㣬��P���˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬��ֱ��д���߶�MN�ij���
![]()
���𰸡���-5+4t;��3��9;�Dz��䣬MN=9
��������
(1)�������⣬��P��ʾ����Ϊ-5+4t��
(2) �ֵ�P��AB֮���˶�ʱ�͵�P���˶�����A���Ҳ�ʱ��������г�������⼴��;
(3) �ֵ�P��AB֮���˶�ʱ�͵�P���˶�����A���Ҳ�ʱ�������,�����е�Ķ�����߶εĺͲ����MN�ij�����.
��1��������ã�BP=4t����P��ʾ������-5+4t��
��2������P��AB֮���˶�ʱ��������ã�
![]()
PB=4t��PA=13-��-5+4t��=18-4 t��
��PB=2PA��
��4t=2��18-4 t����
��t=3;
����P���˶�����A���Ҳ�ʱ��������ã�
![]()
PB=4t��PA=-5+4t-13=4 t -18��
��PB=2PA��
��4t=2��4 t -18����
��t=9;
���Ͽ�֪����P�˶�3���9��ʱ��PB=2PA.
��3������P��AB֮���˶�ʱ��������ã�
![]()
PB=4t��PA=18-4 t��
��MΪBP���е㣬NΪPA���е㣬
��![]() ��
��![]() ,
,
��MN=MP+NP=2t+9-2t=9;
����P���˶�����A���Ҳ�ʱ��������ã�
![]()
PB=4t��PA=4 t -18��
��MΪBP���е㣬NΪPA���е㣬
��![]() ��
��![]() ,
,
��MN=MP-NP=2t-��2t-9��=9;
���Ͽ�֪���߶�MN�ij��Ȳ������仯��������9.


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC��5��AB�Ĵ�ֱƽ����DE�ֱ�AB��AC��E��D.
(1)����BCD���ܳ�Ϊ8����BC�ij���
(2)��BC��4�����BCD���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ����װ���������װÿ����200Ԫ�����ÿ������40Ԫ.������ڼ��̳�������չ���������ڼ���ͻ��ṩ�����Żݷ�����
����һ����һ����װ��һ�������
����������װ������������۵�90%����.
��ij�ͻ�Ҫ�����̳�������װ20�ף����x![]() .
.
��1�����ÿͻ�������һ�����踶�����Ԫ���ú�x��ʽ�ӱ�ʾ�������ÿͻ��������������踶�����Ԫ���ú�x��ʽ�ӱ�ʾ����
��2����![]() ��ͨ������˵����ʱ�����ַ��������Ϊ���㣻
��ͨ������˵����ʱ�����ַ��������Ϊ���㣻
��3����![]() ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ������������.
ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��F��G��H�ֱ�������ABCD���������ϣ���BE=BF=DG=DH������EF��FG��GH��HE�õ��ı���EFGH�� 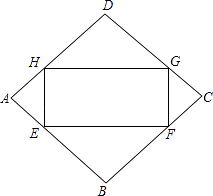
��1����֤���ı���EFGH�Ǿ��Σ�
��2����AB=a����A=60�㣬��BEΪ��ֵʱ������EFGH��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�����˶�Ավ�ڵ�O����ϰ���ţ�������������0.5m��A�����������߳�����A��y���ϣ�������ķ��и߶�y����λ��m�������ʱ��t����λ��s��֮�����㺯����ϵy=at2+5t+c����֪�������0.8sʱ�������ĸ߶�Ϊ3.5m�� 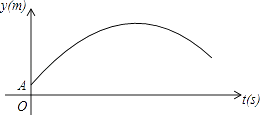
��1��������е�ʱ���Ƕ���ʱ�������������ߣ����߶��Ƕ��٣�
��2����������е�ˮƽ����x����λ��m�������ʱ��t����λ��s��֮����к�����ϵx=10t����֪���ŵĸ߶�Ϊ2.44m��������˶�Ա������������ʱ�������ŵ�ˮƽ����Ϊ28m�����ܷ���ֱ���������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����D��E��F�ֱ���AB��BC��AC���ϣ���BE=CF��BD=CE.
��1����֤����DEF�ǵ��������Σ�
��2������A=40��ʱ�����DEF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����2k��3��x+k2+1=0����������ȵ�ʵ����x1��x2 ��
��1����k��ȡֵ��Χ��
��2����˵��x1��0��x2��0��
��3����������y=x2����2k��3��x+k2+1��x�ύ��A��B���㣬��A����B��ԭ��ľ���ֱ�ΪOA��OB����OA+OB=2OAOB��3����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��Բֱ����D��EΪԲ�������㣬��AD=DE��AE��BD���ڵ�C����ͼ�����BCE��ȵĽ��У� �� 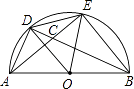
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����![]() ��������Ϊ
��������Ϊ![]() ������ʾ�������ϱ�ʾ��a�ĵ㵽ԭ��ľ��룬���Ǿ���ֵ�ļ������塣��һ���أ������ϵ�������A��B�ֱ�����
������ʾ�������ϱ�ʾ��a�ĵ㵽ԭ��ľ��룬���Ǿ���ֵ�ļ������塣��һ���أ������ϵ�������A��B�ֱ�����![]() ��ʾ����ôA��B����֮��ľ���Ϊ
��ʾ����ôA��B����֮��ľ���Ϊ![]() ����������ʽ��
����������ʽ��![]() �ļ��������ǣ������ϱ�ʾ��
�ļ��������ǣ������ϱ�ʾ��![]() �ĵ�ͱ�ʾ��
�ĵ�ͱ�ʾ��![]() �ĵ�֮��ľ��롣���ô˽��ۣ�
�ĵ�֮��ľ��롣���ô˽��ۣ�![]() ��������������ϱ�ʾ��
��������������ϱ�ʾ��![]() �ĵ㵽��ʾ-2�ͱ�ʾ3�ĵ�ľ���֮����5����
�ĵ㵽��ʾ-2�ͱ�ʾ3�ĵ�ľ���֮����5����![]() �������������
�������������![]() ��
��![]() �ĸ����ǣ� ��
�ĸ����ǣ� ��
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com