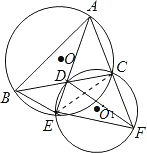
(1)证明:连接两圆的相交弦CE,
在圆O
1中,∠EFD=∠DCE,
在圆O中,∠BAE=∠DCE,
∴∠EFD=∠BAE.
∵AE是∠BAC角平分线,
∴∠BAE=∠CAE.
∴∠CAE=∠EFD.
∵∠AEF=∠FED,
∴△AEF∽△FED.
(2)解:∵△AEF∽△FED,
∴

.
∴EF
2=AE•DE=(AD+DE)•DE=(6+3)×3=27,
∴EF=3

.
(3)解:△ABE为等腰三角形.理由如下:
∵ABCE是圆内接四边形,
∴∠FCE=∠ABE.
∵DF∥BE,∠FDE=∠AEB,
又∵∠FCE=∠EDF,
∴∠AEB=∠ABE.
∴△ABE为等腰三角形.
分析:(1)可通过证两组对应角相等来证两三角形相似.
(2)根据(1)中得出的相似三角形即可得出AE,DE,EF这三条线段的比例关系,有了AD,DE的长,即可求出EF的值.
(3)可通过证角的关系来得出三角形的形状.
点评:本题主要考查了圆周角定理,相似三角形的判定和性质,等腰三角形的性质等知识点.根据圆周角得出相关的角相等是解题的关键.

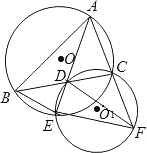 延长线于点F,连接EF、DF.
延长线于点F,连接EF、DF. (1)证明:连接两圆的相交弦CE,
(1)证明:连接两圆的相交弦CE, .
. .
.

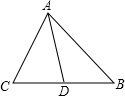 如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.
如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.