
 在△ABC中,AB=AC,O是BC中点,BC=12$\sqrt{3}$cm,AB与⊙O相切于点D,AD:DB=1:3
在△ABC中,AB=AC,O是BC中点,BC=12$\sqrt{3}$cm,AB与⊙O相切于点D,AD:DB=1:3分析 (1)接OD,AO,过O作OE⊥AC于E,由AB与⊙O相切于点D,得到OD⊥AB,∠ODA=90,根据AB=AC,O是BC中点,得到∠AEO=∠ADO=90,通过三角形全等得到OD=OE,问题即可得证;
(2)由AB=AC,O是BC中点,得到AO⊥BC,由于∠1+∠2=∠2+∠3=90°,所以∠1=∠3,通过△ADO∽△ODB,得到$\frac{AD}{OD}$=$\frac{OD}{BD}$,设AD=x,BD=3x,在Rt△ADO中,tan∠2=$\frac{AD}{OD}$=$\frac{x}{\sqrt{3}x}$$\frac{\sqrt{3}}{3}$,求出∠2=30°∠3=60°得到∠DOC=120°于是求得S阴影=S△ABC-S△BOD-S扇形DOF=$\frac{1}{2}×12\sqrt{3}×3\sqrt{3}-\frac{1}{2}×9×3\sqrt{3}$-$\frac{120π{•(3\sqrt{3})}^{2}}{360}$=54-$\frac{27\sqrt{3}}{2}$-9π.
解答  解:(1)连接OD,AO,过O作OE⊥AC于E,
解:(1)连接OD,AO,过O作OE⊥AC于E,
∵AB与⊙O相切于点D,
∴OD⊥AB,∴∠ODA=90°,
∵AB=AC,O是BC中点,
∴∠AEO=∠ADO=90°,
在△AOD与△AOE中,
$\left\{\begin{array}{l}{∠BAO=∠CAO}\\{∠AEO=∠ADO}\\{AO=AO}\end{array}\right.$,
∴△ADO≌△AOE(AAS),
∴OD=OE,
∴AC与⊙O相切;
(2)∵AB=AC,O是BC中点,
∴AO⊥BC,
∵∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
∵∠ADO=∠BDO=90°,
∴△ADO∽△ODB,
∴$\frac{AD}{OD}$=$\frac{OD}{BD}$,
∴OD2=AD•BD,
∵AD:DB=1:3,
∴设AD=x,BD=3x,
∴OD2=x•3x,
∴$OD=\sqrt{3}x$,
在Rt△ADO中,tan∠2=$\frac{AD}{OD}$=$\frac{x}{\sqrt{3}x}$$\frac{\sqrt{3}}{3}$,
∴∠2=30°∠3=60°,
∴∠DOC=120°,
∵BC=12$\sqrt{3}$,
∴BO=6$\sqrt{3}$,
∴OD=$\frac{6\sqrt{3}}{2}$=3$\sqrt{3}$,BD=3$\sqrt{3}$$•\sqrt{3}$=9,
∴S阴影=S△ABC-S△BOD-S扇形DOF=$\frac{1}{2}×12\sqrt{3}×3\sqrt{3}-\frac{1}{2}×9×3\sqrt{3}$-$\frac{120π{•(3\sqrt{3})}^{2}}{360}$=54-$\frac{27\sqrt{3}}{2}$-9π.
点评 本题考查了切线的判定和性质,全等三角形的判定与性质,相似三角形的判定和性质,锐角三角函数,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2m}$+$\sqrt{3m}$=$\sqrt{5m}$ | B. | 5$\sqrt{5}$-$\sqrt{5}$=4 | C. | 5+$\sqrt{2}$=5$\sqrt{2}$ | D. | m$\sqrt{x}$-n$\sqrt{x}$=(m-n)$\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
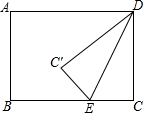 如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.
如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一块梯形空地ABCD可供停车,AD∥BC,∠C=90°,∠B=53°,AD=1.6m,CD=5.2m,现有一辆长4.9m,宽1.9m的汽车需要完全停入梯形区域,请你设计一种停车方案,并通过计算说明理由.(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)
如图,有一块梯形空地ABCD可供停车,AD∥BC,∠C=90°,∠B=53°,AD=1.6m,CD=5.2m,现有一辆长4.9m,宽1.9m的汽车需要完全停入梯形区域,请你设计一种停车方案,并通过计算说明理由.(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A(2,2)在双曲线y1=$\frac{k}{x}$(x>0)上,点C在双曲线y2=-$\frac{9}{x}$(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
如图,点A(2,2)在双曲线y1=$\frac{k}{x}$(x>0)上,点C在双曲线y2=-$\frac{9}{x}$(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G,铁塔EF的高为(10.6+3$\sqrt{3}$)米.(结果用带根号的式子表示)
如图,为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G,铁塔EF的高为(10.6+3$\sqrt{3}$)米.(结果用带根号的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
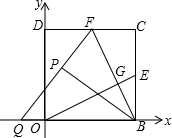 如图,在平面直角坐标系中,正方形OBCD的点B的坐标为(2,0),E,F分别为边BC,CD上的点,且BE=CF,连结OE,BF,交点为G,将△BCF沿BF对折,得到△BPF,延长FP交x轴于点Q.
如图,在平面直角坐标系中,正方形OBCD的点B的坐标为(2,0),E,F分别为边BC,CD上的点,且BE=CF,连结OE,BF,交点为G,将△BCF沿BF对折,得到△BPF,延长FP交x轴于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com