
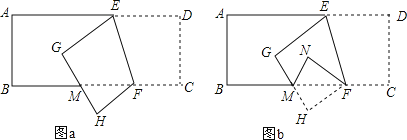
【题目】如图a,已知长方形纸带ABCD,AB∥CD,AD∥BC,∠BFE=70°,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b.
(1)图a中,∠AEG=______°;
(2)图a中,∠BMG=______°;
(3)图b中,∠EFN=______°.
【答案】(1)40°;(2)50°;(3)30°.
【解析】
(1)根据平行线的性质求出∠DEF的度数,由折叠的性质和平角的定义即可得出结论;
(2)由(1)知,∠HFM=40°,再由翻折变换的性质得出∠H=∠C=90°,由三角形内角和定理得出∠HMF的度数,根据对顶角相等即可得出结论;
(3)先根据图形翻折变换的性质得出∠MFN=∠HFM=40°,再由∠BFE=70°即可得出结论.
(1)∵∠BFE=70°,AD∥BC,
∴∠DEF=∠BFE=70°,
∴∠GEF=∠DEF=70°,
∴∠AEG=180°-70°-70°=40°.

(2)∵由(1)知,∠HFM=40°,∠H=∠C=90°,
∴∠HMF=90°-40°=50°.
∵∠HMF与∠BMG是对顶角,
∴∠BMG=∠HMF=50°.
(3)∵△MNF由△MHF翻折而成,
∴∠MFN=∠HFM=40°,
∵∠BFE=70°,
∴∠EFN=∠BFE-∠MFN=70°-40°=30°.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯目前是世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )
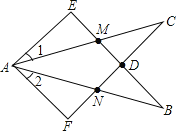
A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:二元一次方程![]() 有无数组解,每组解记为
有无数组解,每组解记为![]() ,称
,称![]() 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
(1) 已知![]() ,则是隐线
,则是隐线![]() 的亮点的是 ;
的亮点的是 ;
(2) 设![]() 是隐线
是隐线![]() 的两个亮点,求方程
的两个亮点,求方程![]() 中
中![]() 的最小的正整数解;
的最小的正整数解;
(3)已知![]() 是实数, 且
是实数, 且![]() ,若
,若![]() 是隐线
是隐线![]() 的一个亮点,求隐线
的一个亮点,求隐线![]() 中的最大值和最小值的和.
中的最大值和最小值的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[m]为不大于m的最大整数;
(1)填空:[3.2]= ,[﹣4.8]= ;
(2)已知:动点C在数轴上表示数a,且﹣2≤[a]≤4,则a的取值范围 ;
(3)如图:OB=1,AB⊥OB,且AB=10,动点D在数轴上表示的数为t,设AD﹣BD=n,且6≤[n]≤7,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作AC的垂直平分线,交AB于点O,交AC于点D;
②以O为圆心,OA为半径作圆,交OD的延长线于点E.
(2)在(1)所作的图形中,解答下列问题.
①点B与⊙O的位置关系是__;(直接写出答案)
②若DE=2,AC=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,若满足下列条件,则一定不是直角三角形的是( )
中,若满足下列条件,则一定不是直角三角形的是( )
A.∠A=∠B+∠CB.∠A=∠C-∠B
C.一个外角等于与它相邻的内角D.∠A∶∠B∶∠C=1∶3∶5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com