
如图,矩形OABC的顶点B的坐标为(1,2),反比例函数y= (0<m<2)的图象与AB交于点E,与BC交于点F,连接OE、OF、EF.
(0<m<2)的图象与AB交于点E,与BC交于点F,连接OE、OF、EF.
(1)若点E是AB的中点,则m= ,S△OEF= ;
(2)若S△OEF=2S△BEF,求点E的坐标;
(3)是否存在点E及y轴上的点M,使得△MFE与△BFE全等?若存在,写出此时点E的坐标;若不存在,说明理由.
(1)m=1;S△OEF= ;
;
(2)点E的坐标为(1, )
)
(3)存在;E点坐标为(1, )
)
解析试题分析:(1)先得到E点坐标为(1,1),然后根据反比例函数图象上点的坐标特征即可得到k=1,再利用F的纵坐标为2可确定F点坐标为(  ,2),则可根据S△OEF=S矩形ABCO-S△AOE-S△OCF-S△BEF进行计算;
,2),则可根据S△OEF=S矩形ABCO-S△AOE-S△OCF-S△BEF进行计算;
(2)由题意,E(1,m),F( ,2),可表示出△BEF的面积,进而可表示出△OEF与△BEF的面积之和,从而可得到m的值,进而得到点E的坐标;
,2),可表示出△BEF的面积,进而可表示出△OEF与△BEF的面积之和,从而可得到m的值,进而得到点E的坐标;
作EH⊥y轴于C,如图,设E点坐标为(1,m),则F( ,2),:
,2),:
由于m<2,则由△MFE≌△BFE得到MF="BF=1-m"
ME=BE=2-m,∠FME=90°,易证得Rt△CFM∽Rt△HME,利用相似比可得到MH=m,然后在Rt△MHM中,根据勾股定理得12+m2=(2-km)2,解得m= ,则E点坐标为(1,
,则E点坐标为(1, )
)
试题解析:(1)∵B点坐标为(1,2),点E是AB的中点,AB⊥X轴,
∴E点坐标为(1,1),
∵点E在函数为y= 上,
上,
∴1= ,
,
∴m=1
把y=2代入y= 得
得 =2,解得x=
=2,解得x= ,
,
∴F点坐标为( ,2),
,2),
∴S△OEF=S矩形ABCO-S△AOE-S△OCF-S△BEF
=1×2- ×1×1 -
×1×1 - ×
× ×2-
×2- ×
× × 1
× 1
= ;
;
(2)根据题意,E(1,m),F( ,2)
,2)
∴S△BEF= ,
,
∵S△OAE=S△OCF=
∴S△BEF+S△OEF=2-m,
∵S△OEF=2S△BEF,
∴S△BEF= ,
,
∴ =
= ,
,
解得,m=2(舍去),或m=
∴点E的坐标为(1, )
)
(3)作EH⊥y轴于C,如图,
设E点坐标为(1,m),则F( ,2),
,2),
当m<2时,
∵△MFE≌△BFE,
∴MF=BF=1- ,ME=BE=2-m,∠FME=90°,
,ME=BE=2-m,∠FME=90°,
∴Rt△CFM∽Rt△HME,
∴MF:ME=CF:MH,
∴MH= =m,
=m,
在Rt△MHM中,HE=1,
∴HE2+MH2=ME2,
∴12+m2=(2-m)2,解得m= ,
,
∴E点坐标为(1, )
)
考点:1、反比例函数图象上点的坐标特征;2、三角形全等的性质和矩形性质;3、勾股定理;4、相似比


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数 的图象上,第二象限内的点B在反比例函数
的图象上,第二象限内的点B在反比例函数 的图象上,连接OA、OB,若OA⊥OB,OB=
的图象上,连接OA、OB,若OA⊥OB,OB= OA,则k= .
OA,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数 位于第一象限的图象上,则k的值为 .
位于第一象限的图象上,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
如图,是反比例函数 的图象的一支.根据给出的图象回答下列问题:
的图象的一支.根据给出的图象回答下列问题:
(1)该函数的图象位于哪几个象限?请确定m的取值范围;
(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,经过原点的两条直线 、
、 分别与双曲线
分别与双曲线 相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
(1)求 值及
值及 点坐标;(4分)
点坐标;(4分)
(2)若P点坐标为(a,3),求a值及四边形APBQ的面积;(4分)
(3)若P点坐标为(m,n),且 ,求P点坐标.(4分)
,求P点坐标.(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
对于平面直角坐标系xOy中的点P(a,b),若点 的坐标为(
的坐标为( ,
,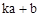 )(其中k为常数,且
)(其中k为常数,且 ),则称点
),则称点 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为 (1+
(1+ ,
, ),即
),即 (3,6).
(3,6).
(1)①点P 的“2属派生点”
的“2属派生点”  的坐标为____________;
的坐标为____________;
②若点P的“k属派生点”  的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
(2)若点P在x轴的正半轴上,点P的“k属派生点”为 点,且△
点,且△ 为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________;
(3)如图, 点Q的坐标为(0, ),点A在函数
),点A在函数 的图象上,且点A是点B的“
的图象上,且点A是点B的“ 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
完成y= 的图象,并根据图象回答问题.
的图象,并根据图象回答问题.
(1)根据图象指出,当y=-2时x的值;
(2)根据图象指出,当-2<x<1时,y的取值范围;
(3)根据图象指出,当-3<y<2时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com