
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图①,当∠BOC=40°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化,说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出∠DOE的度数(不必写过程).
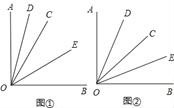
【答案】(1)45°;(2)∠DOE的大小不变,理由见解析;(3)45°或135°;画图见解析.
【解析】
(1)如图①,当∠BOC=40°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化,说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数(不必写出过程).
解:(1)如图,∠AOC=90°﹣∠BOC=50°,
∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC=25°,∠COE=
∠AOC=25°,∠COE=![]() ∠BOC=20°,
∠BOC=20°,
∴∠DOE=∠COD+∠COE=45°;
(2)∠DOE的大小不变,理由是:
∠DOE=∠COD+∠COE=![]() ∠AOC+
∠AOC+![]() ∠COB=
∠COB=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ∠AOB=45°;
∠AOB=45°;
(3)∠DOE的大小发生变化情况为,
如图3,则∠DOE为45°;如图4,则∠DOE为135°,

分两种情况:如图3所示,
∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD﹣∠COE=![]() (∠AOC﹣∠BOC)=45°;
(∠AOC﹣∠BOC)=45°;
如图4所示,∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ×270°=135°.
×270°=135°.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小李同学勤工俭学购进一批矿泉水和运动饮料在运动场进行销售,其进价与售价如下表:
进价(元/瓶) | 售价(元/瓶) | |
矿泉水 | 0.75 | 2 |
运动饮料 | 3 | 4 |
(1)若小李同学购进矿泉水和运动饮料共 30 瓶,用去了 67.5 元,并且全部售完,问小李同学在该买卖中赚了多少钱?
(2)为了进一步满足同学们的需求,小李同学决定用不超过 400 元的资金购进矿泉水和运动饮料共200 瓶,问最多购进多少瓶运动饮料?
(3)小李同学赚钱后,为了回报社会,买了一批书籍送给贫困山区的孩子,如果分给每位孩子 4 本书,那么剩下 10 本书;如果分给每位孩子 5 本书,那么最后一位孩子分得的书不足 4 本,但至少1本,则小李同学买了多少本书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对A、B两款运动鞋的销售情况进行了为期5天的统计,得到了这两款运动鞋每天的销售量及总销售额统计图(如图所示).已知第4天B款运动鞋的销售量是A款的![]() .
.

(1)求第4天B款运动鞋的销售量.
(2)这5天期间,B款运动鞋每天销售量的平均数和中位数分别是多少?
(3)若在这5天期间两款运动鞋的销售单价保持不变,求第3天的总销售额(销售额=销售单价×销售量).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同,甲商场规定:凡超过![]() 元的电器,超出的金额按
元的电器,超出的金额按![]() 收取;乙商场规定:凡超过
收取;乙商场规定:凡超过![]() 元的电器,超出的金额按
元的电器,超出的金额按![]() 收取,某顾客购买的电器价格是
收取,某顾客购买的电器价格是![]() 元.
元.
(1)当![]() 时,分别用代数式表示在两家商场购买电器所需付的费用
时,分别用代数式表示在两家商场购买电器所需付的费用
(2)当![]() 时,该顾客应选择哪一家商场购买比较合算?说明理由.
时,该顾客应选择哪一家商场购买比较合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填空或填写适当的理由:
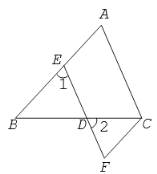
(1)![]() ,(已知)
,(已知)
![]() ______________.(___________________________________________)
______________.(___________________________________________)
![]() ________________
________________![]() (______________________________________)
(______________________________________)
(2)![]() _______,(已知)
_______,(已知)
![]() ;(___________________________________)
;(___________________________________)
(3)![]() _______________,(已知)
_______________,(已知)
![]() ___________
___________![]() _______________.(_______________________________)
_______________.(_______________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=60°,求∠2、∠3的度数;
(2)若点![]() 是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系:
是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系:
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;请阅读下面的解答过程,并填空(理由或数学式).

解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB( )
∵AB∥CD(已知),MN∥AB(作图),
∴MN∥CD( )
∴∠MPF=∠PFD( )
∴ =∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD.
②当点P在图3的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系: ;
查看答案和解析>>
科目:初中数学 来源: 题型:
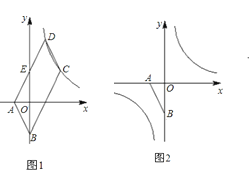
【题目】如图1,已知点A(a,0),B(0,b),且a、b满足![]() , ABCD的边AD与y轴交于点E,且E为AD中点,双曲线
, ABCD的边AD与y轴交于点E,且E为AD中点,双曲线![]() 经过C、D两点.
经过C、D两点.
(1)求k的值;
(2)点P在双曲线![]() 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com