
���� ��1���ֱ���y=0��x=0����y=-x+4�������B��C�����꣬Ȼ���������ߵĽ���ʽΪy=a��x+2����x-4��������C��������������߽���ʽ�������a��ֵ�Ͷ���D�����ꣻ
��2�����ı���DEFPΪƽ���ı���ʱ����DP��BC����ֱ��DP�Ľ���ʽΪy=mx+n����m=-1�����ֱ��DP�Ľ���ʽ�����������߽���ʽ��ֱ��DP�Ľ���ʽ�������P�����ꣻ
��3���������֪��0��t��6������QMNΪ����ֱ�������Σ���������������١�NMQ=90�㣻�ڡ�MNQ=90�㣻�ۡ�NQM=90�㣮
��� �⣺��1����x=0����y=-x+4
��y=3��
��C��0��3����
��y=0����y=-x+4����
��x=4��
��B��4��0����
�������ߵĽ���ʽΪ��y=a��x+2����x-4����
��C��0��4������y=a��x+2����x-4����
��a=-$\frac{1}{2}$��
�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$��x+2����x-4��=-$\frac{1}{2}$x2+x+4��
�ඥ��D������Ϊ��1��$\frac{9}{2}$����
��2����DP��BCʱ��
��ʱ�ı���DEFP��ƽ���ı��Σ�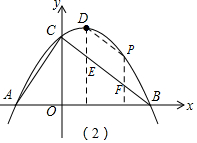
��ֱ��DP�Ľ���ʽΪy=mx+n��
��ֱ��BC�Ľ���ʽΪ��y=-x+4��
��m=-1��
��y=-x+n��
��D��1��$\frac{9}{2}$������y=-x+n��
��n=$\frac{11}{2}$��
��ֱ��DP�Ľ���ʽΪy=-x+$\frac{11}{2}$��
������ $\left\{\begin{array}{l}{y=-x+\frac{11}{2}}\\{y=-\frac{1}{2}{x}^{2}+x+4}\end{array}\right.$��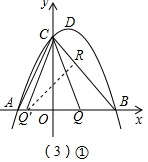
��ã�x=3��x=1����ȥ����
���x=3����y=-x+$\frac{11}{2}$��
y=$\frac{5}{2}$��
��P��������3��$\frac{5}{2}$����
��3������ͼ������BQC=120��ʱ�����CQO=60�㣬
��OQ=$\frac{4}{3}$$\sqrt{3}$��
��t=4-$\frac{4}{3}$$\sqrt{3}$��
����CQ��B=75��ʱ����Q����Q��R��BC��R��
��BR=RQ��=$\frac{\sqrt{2}}{2}$t��CR=$\frac{\sqrt{6}}{6}$t��
��$\frac{\sqrt{2}}{2}$t$+\frac{\sqrt{6}}{6}$t=4$\sqrt{2}$��
��t=12-4$\sqrt{3}$��
��75�㣼��BQC��120�㣬
�˶�ʱ��t���룩�ķ�Χ��4-$\frac{4}{3}$$\sqrt{3}$��t��12-4$\sqrt{3}$��
�ʴ�Ϊ��4-$\frac{4}{3}$$\sqrt{3}$��t��12-4$\sqrt{3}$��
���������֪��0��t��6��
��ֱ��AC�Ľ���ʽΪ��y=mx+n��
��A��-2��0����C��0��4������y=mx+n��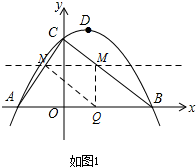
�ã�$\left\{\begin{array}{l}{0=-2m+n}\\{4=n}\end{array}\right.$��
���� $\left\{\begin{array}{l}{m=2}\\{n=4}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪ��y=2x+4��
������֪��QB=t��
��ͼ1������NMQ=90�㣬
��OQ=4-t��
��x=4-t����y=-x+4��
��y=t��
��M��4-t��t����
��MN��x�ᣬ
��N��������Ϊ t��
��y=t����y=2x+4��
��x=$\frac{1}{2}$t-2��
��N�� $\frac{1}{2}$t-2��t����
��MN=��4-t��-��$\frac{1}{2}$t-2��=6-$\frac{3}{2}$t��
��MQ��OC��
���BQM�ס�BOC��
��$\frac{MQ}{OC}$=$\frac{QB}{OB}$��
��MQ=t��
��MN=MQʱ��
��6-$\frac{3}{2}$t=t��
��t=$\frac{12}{5}$��
��ʱQB=$\frac{12}{5}$���������⣬
��ͼ2������QNM=90��ʱ��
��QB=t��
���Q��������4-t��0��
����x=4-t����y=2x+4��
��y=12-2t��
��N��4-t��12-2t����
��MN��x�ᣬ
���M��������Ϊ12-2t��
����y=12-2t����y=-x+4��
��x=2t-8��
��M��2t-8��12-2t����
��MN=��2t-8��-��4-t��=3t-12��
��NQ��OC��
���AQN�ס�AOC��
��$\frac{NQ}{OC}$=$\frac{AQ}{OA}$��
��NQ=12-2t��
��NQ=MNʱ��
��12-2t=3t-12��
��t=$\frac{24}{5}$��
���ʱQB=$\frac{24}{5}$���������⣬
��ͼ3������NQM=90�㣬
����Q��QE��MN�ڵ�E��
����M��MF��x���ڵ�F��
��QE=a��
��y=a����y=-x+4��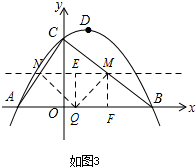
��x=4-a��
��M��4-a��a����
��y=a����y=2x+4��
��x=$\frac{1}{2}$a-2��
��N�� $\frac{1}{2}$a-2��a����
��MN=��4-a��-�� $\frac{1}{2}$a-2��=6-$\frac{3}{2}$a��
��MN=2QEʱ��
��6-$\frac{3}{2}$a=2a��
��a=$\frac{12}{7}$��
��MF=QE=$\frac{12}{7}$��
��MF��OC��
���BMF�ס�BCO��
��$\frac{MF}{OC}$=$\frac{BF}{OB}$��
��BF=$\frac{12}{7}$��
��QB=QF+BF=$\frac{24}{7}$��
��t=$\frac{24}{7}$��������������⣬
��������������QMNΪ����ֱ��������ʱ����ʱt=$\frac{12}{5}$��$\frac{24}{5}$�� $\frac{24}{7}$��
���� ���⿼����κ������ۺ����⣬�漰����ϵ������һ�κ����Ͷ��κ����Ľ���ʽ�������������ж������ʣ�����ֱ�������ε�����֪ʶ��Ҫ���������ν�ϵ�˼��Ѵ����ͼ���ͼ�ν�����������õ������������ʾ�߶εij��ȣ��Ӷ�����߶�֮��Ĺ�ϵ��


 С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д� ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{2}$+2 | C�� | $\sqrt{2}$+1 | D�� | 2$\sqrt{2}$+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
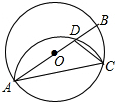 ��ͼ��ABΪ��O��ֱ������CΪԲ��һ�㣬��BAC=25�㣬�����ӻ�$\widehat{AC}$����AC���۽�AB�ڵ�D������CD�����DCA�Ķ���Ϊ��������
��ͼ��ABΪ��O��ֱ������CΪԲ��һ�㣬��BAC=25�㣬�����ӻ�$\widehat{AC}$����AC���۽�AB�ڵ�D������CD�����DCA�Ķ���Ϊ��������| A�� | 35�� | B�� | 40�� | C�� | 45�� | D�� | 50�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
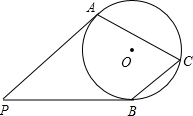 ��ͼ��PA��PB�ǡ�O�����ߣ��е�ֱ�ΪA��B����C�ڡ�O�ϣ���$\widehat{ACB}$���Ż������ACB���ڣ�������
��ͼ��PA��PB�ǡ�O�����ߣ��е�ֱ�ΪA��B����C�ڡ�O�ϣ���$\widehat{ACB}$���Ż������ACB���ڣ�������| A�� | 180��-2��P | B�� | 180��-��P | C�� | 90��-$\frac{1}{2}$��P | D�� | ��P |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x3+x3=x6 | B�� | ��3a��2����3a-2��=1 | C�� | ��-a��3•a2=-a6 | D�� | ��-4m2n��2=16m4n2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 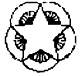 | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com