
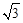 ]ŁŹFZ[60ĄăŁŹ2+
]ŁŹFZ[60ĄăŁŹ2+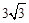 ]ĄŁ
]ĄŁ ĄÏAOC=45ĄăŁŹĄàFZ[45ĄăŁŹ3]ĄŁ
ĄÏAOC=45ĄăŁŹĄàFZ[45ĄăŁŹ3]ĄŁ
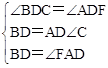 ŁŹ
ŁŹ CF=CDĄŁ
CF=CDĄŁ ĄÏCOD=30ĄăĄŁ
ĄÏCOD=30ĄăĄŁ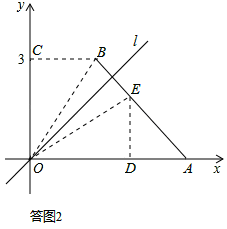
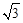 ]ŁŹFZ[60ĄăŁŹ2+
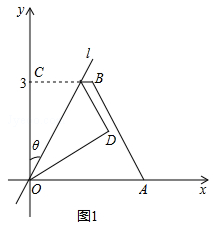
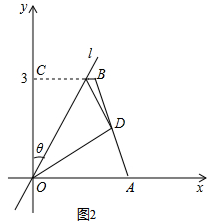
]ŁŹFZ[60ĄăŁŹ2+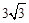 ]ĄŁÈçŽđÍŒ3ĄąŽđÍŒ4ËùÊŸĄŁ
]ĄŁÈçŽđÍŒ3ĄąŽđÍŒ4ËùÊŸĄŁ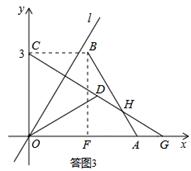



 ”„ÔȘÆÚÖĐÆÚÄ©ŸíÏ”ÁĐŽđ°ž
”„ÔȘÆÚÖĐÆÚÄ©ŸíÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁșČ»Ïê ÌâĐÍŁșÌîżŐÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁșČ»Ïê ÌâĐÍŁșÌîżŐÌâ
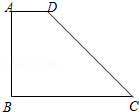
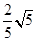 ŁšŒŽcosC=
ŁšŒŽcosC=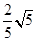 Ł©ŁŹÔòAC±ßÉÏ”ÄÖĐÏßł€ÊÇ Łź
Ł©ŁŹÔòAC±ßÉÏ”ÄÖĐÏßł€ÊÇ ŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁșČ»Ïê ÌâĐÍŁș”„ŃĄÌâ
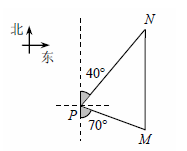
| AŁź40șŁÀï | BŁź60șŁÀï | CŁź70șŁÀï | DŁź80șŁÀï |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁșČ»Ïê ÌâĐÍŁșÌîżŐÌâ
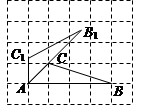
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com