
【题目】2019年3月30日,四川省凉山州木里县境内发生森林火灾,30名左右的扑火英雄牺牲,让人感到痛心,也再次给我们的防火安全意识敲响警钟.为了加强学生的防火安全意识,某校举行了一次“防火安全知识竞赛”(满分100分),赛后从中抽取了部分学生的成绩进行整理,并制作了如下不完整的统计图表:
组别 | 成绩x/分 | 组中值 |
A | 50≤x<60 | 55 |
B | 60≤x<70 | 65 |
C | 70≤x<80 | 75 |
D | 80≤x<90 | 85 |
E | 90≤x<100 | 95 |
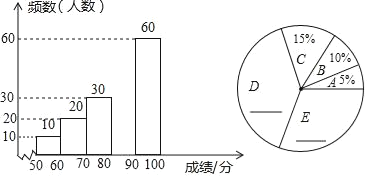
请根据图表提供的信息,解答下列各题:
(1)补全频数分布直方图和扇形统计图;
(2)分数段80≤x<90对应扇形的圆心角的度数是 °,所抽取的学生竞赛成绩的中位数落在 区间内;
(3)若将每组的组中值(各组两个端点的数的平均数)代表各组每位学生的竞赛成绩,请你估计该校参赛学生的平均成绩.
【答案】(1)详见解析;(2)144,80≤x<90;(3)估计该校参赛学生的平均成绩是83分.
【解析】
(1)用A组的人数除以所占的百分比得出抽取的学生总数,再用数据总数减去A、B、C、E四个组的人数可得D组人数,补全频数分布直方图;用D组人数除以数据总数得出D组所占百分比,同理求出E组所占百分比,补全扇形统计图;
(2)用360°乘以D组所占百分比即可求出分数段80≤x<90对应扇形的圆心角的度数;根据中位数的定义,将这组数据按照从小到大的顺序排列后,处于中间位置的数据(或中间两数据的平均数)即为中位数;
(3)先利用加权平均数的计算公式求出样本平均数,再利用样本估计总体的思想解决问题即可.
解:(1)样本容量是:10÷5%=200,
D组人数是:200﹣(10+20+30+60)=80(人),
D组所占百分比是:![]() ×100%=40%,
×100%=40%,
E组所占百分比是:![]() ×100%=30%.
×100%=30%.
补全频数分布直方图和扇形统计图如图所示:

(2)分数段80≤x<90对应扇形的圆心角的度数是:360°×0.40=144°;
一共有200个数据,按照从小到大的顺序排列后,第100个与第101个数据都落在D组,
所以所抽取的学生竞赛成绩的中位数落在80≤x<90区间内.
故答案为144,80≤x<90;
(3)(55×10+65×20+75×30+85×80+95×60)÷200=83(分).
所以估计该校参赛学生的平均成绩是83分.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax﹣1的图象与反比例函数y=![]() 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=
的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=![]() ,tan∠AOC=
,tan∠AOC=![]() .
.
(1)求a,k的值及点B的坐标;
(2)观察图象,请直接写出不等式ax﹣1≥![]() 的解集;
的解集;
(3)在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标.
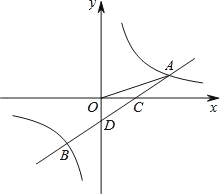
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春晓中学为开展“校园科技节”活动,计划购买A型、B型两种型号的航模.若购买8个A型航模和5个B型航模需用2200元;若购买4个A型航模和6个B型航模需用1520元.求A,B两种型号航模的单价分别是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,CA=CB,0°<∠ACB≤90°,点M、N分别在边CA,CB上(不与端点重合),BN=AM,射线AG∥BC交BM延长线于点D,点E在直线AN上,EA=ED.
(1)(观察猜想)如图1,点E在射线NA上,当∠ACB=45°时,①线段BM与AN的数量关系是 ; ②∠BDE的度数是 ;
(2)(探究证明)如图2点E在射线AN上,当∠ACB=30°时,判断并证明线段BM与AN的数量关系,求∠BDE的度数;
(3)(拓展延伸)如图3,点E在直线AN上,当∠ACB=60°时,AB=3,点N是BC边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.
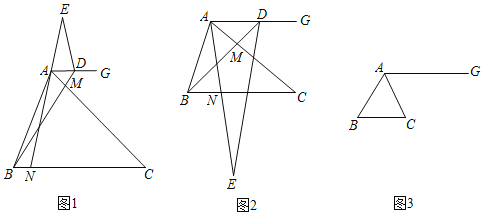
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
(1)如图①,已知线段AB和BC,AB=2,BC=5,则线段AC的最小值为 ;
问题探究
(2)如图②,已知扇形COD中,∠COD=90°,DO=CO=6,点A是OC的中点,延长OC到点F,使CF=OC,点P是![]() 上的动点,点B是OD上的一点,BD=1.
上的动点,点B是OD上的一点,BD=1.
(i)求证:△OAP~△OPF;
(ii)求BP+2AP的最小值;
问题解决:
(3)如图③,有一个形状为四边形ABCD的人工湖,BC=9千米,CD=4![]() 千米,∠BCD=150°,现计划在湖中选取一处建造一座假山P,且BP=3千米,为方便游客观光,从C、D分别建小桥PD,PC.已知建桥PD每千米的造价是3万元,建桥PC每千米的造价是1万元,建桥PD和PC的总造价是否存在最小值?若存在,请确定点P的位置并求出总造价的最小值,若不存在,请说明理由.(桥的宽度忽略不计)
千米,∠BCD=150°,现计划在湖中选取一处建造一座假山P,且BP=3千米,为方便游客观光,从C、D分别建小桥PD,PC.已知建桥PD每千米的造价是3万元,建桥PC每千米的造价是1万元,建桥PD和PC的总造价是否存在最小值?若存在,请确定点P的位置并求出总造价的最小值,若不存在,请说明理由.(桥的宽度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC与⊙O相切于点B,CD与⊙O相切于点D,连结AD.
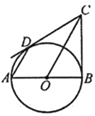
(1)求证:AD∥OC.
(2)小聪与小明在做这个题目的时候,对∠CDA与∠AOC之间的关系进行了探究:
小聪说,∠CDA+∠AOC的值是一个固定的值;
小明说,∠CDA+∠AOC的值随∠A度数的变化而变化.
若∠CDA+∠AOC的值为y,∠A度数为x.你认为他们之中谁说的是正确的?若你认为小聪说的正确,请你求出这个固定值:若你认为小明说的正确,请你求出y与x之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC于点 D.
(1)求抛物线的函数表达式;
(2)当AD=2PD时,求点P的坐标;
(3)求线段PE的最大值;
(4)当线段PE最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永康市某校在课改中,开设的选修课有:篮球,足球,排球,羽毛球,乒乓球,学生可根据自己的爱好选修一门,李老师对九(1)班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
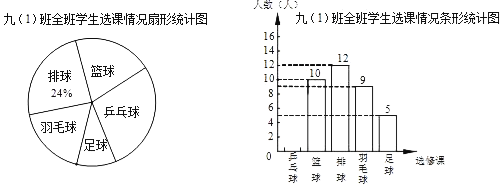
(1)该班共有学生 人,并补全条形统计图;
(2)求“篮球”所在扇形圆心角的度数;
(3)九(1)班班委4人中,甲选修篮球,乙和丙选修足球,丁选修排球,从这4人中任选2人,请你用列表或画树状图的方法,求选出的2人中恰好为1人选修篮球,1人选修足球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com