
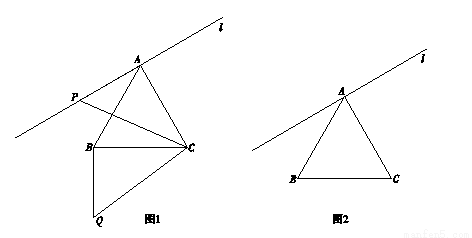
如图,等边三角形ABC的边长为4,直线l经过点A并与AC垂直.当点P在直线l上运动到某一位置(点P不与点A重合)时,连接PC,并将△ACP绕点C按逆时针方向旋转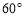 得到△BCQ,记点P的对应点为Q,线段PA的长为m(
得到△BCQ,记点P的对应点为Q,线段PA的长为m(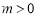 ).
).
(1)①∠QBC= 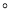 ;
;
② 如图1,当点P与点B在直线AC的同侧,且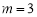 时,点Q到直线l的距离等于 ;
时,点Q到直线l的距离等于 ;
(2)当旋转后的点Q恰好落在直线l上时,点P,Q的位置分别记为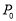 ,
,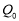 .在图2中画出此时的线段
.在图2中画出此时的线段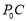 及△
及△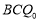 ,并直接写出相应m的值;
,并直接写出相应m的值;
(3)当点P与点B在直线AC的异侧,且△PAQ的面积等于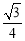 时,求m的值.
时,求m的值.
(1)①90°;②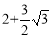 ;(2)作图见试题解析,
;(2)作图见试题解析,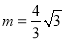 ;(3)
;(3)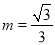 或
或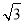 或
或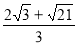 .
.
【解析】
试题分析:(1)由旋转的性质,得到∠QBC=∠PAC=90°;
②过Q作QM⊥l于点M,延长AB交MQ于点N,过点N作NO⊥BQ于点O,可以得到∠NBQ=∠NQB=30°,得到NB=NQ,解直角三角形BNO得到NB=NQ= ,得到AN=
,得到AN=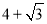 ,在△AMN中,得到MN的值,从而得到MQ的长;
,在△AMN中,得到MN的值,从而得到MQ的长;
(2)所画图形如图.由∠BAC=60°,∠CAQ0=90°,得到∠Q0AB=30°,同理有∠Q0BA=30°,得到Q0B= Q0A= P0A=m,在△Q0BC和△Q0AC中,由于 Q0B=Q0A,Q0C=Q0C,BC=AC,故△Q0BC≌△Q0AC,得到∠Q0CB=∠Q0CA=30°,从而计算出Q0B的长;
(3)作BG⊥AC于点G,过点Q作直线l的垂线交l于点D,交BG于点F,可以求出 QF=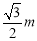 ,要使△PAQ存在,则点P不能与点A,
,要使△PAQ存在,则点P不能与点A,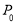 重合,所以点P的位置分为以下两种情况:
重合,所以点P的位置分为以下两种情况:
①如图2,当点P在(2)中的线段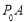 上(点P不与点A,
上(点P不与点A,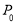 重合)时,可得
重合)时,可得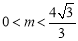 ,此时点Q在直线l的下方.得到 DQ=DF-QF=
,此时点Q在直线l的下方.得到 DQ=DF-QF=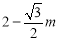 .根据三角形面积公式有:
.根据三角形面积公式有: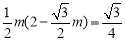 .解方程可以得到m的值;
.解方程可以得到m的值;
②如图3,当点P在(2)中的线段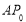 的延长线上(点P不与点A,
的延长线上(点P不与点A,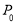 重合)时,可得
重合)时,可得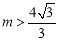 ,此时点Q在直线l的上方.此时DQ=QF-DF=
,此时点Q在直线l的上方.此时DQ=QF-DF= 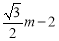 .根据三角形面积公式有:.
.根据三角形面积公式有:.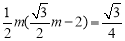 .解方程可以得到m的值.
.解方程可以得到m的值.
试题解析:【解析】
(1)①由旋转的性质,得到△QBC≌△PAC,∠QBC=∠PAC=90°;
②过Q作QM⊥l于点M,延长AB交MQ于点N,过点N作NO⊥BQ于点O,如图,∵∠BAC=60°,∠CAP=90°,∴∠PAB=30°,∠ANM=60°,∵∠CBQ=90°,,∠ABC=60°,∴∠NBQ=30°,∴∠NQB=30°,∴NB=NQ,∵BQ=AM=3,∴BO=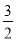 ,∴NO=
,∴NO=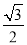 ,∴NB=NQ=
,∴NB=NQ= ,∵AB=4,∴AN=
,∵AB=4,∴AN=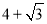 ,∴MN=
,∴MN=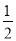 AN=
AN=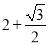 ,∴MQ=MN+NQ=
,∴MQ=MN+NQ=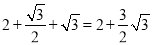 .故当 m=3时,点Q到直线l的距离等于
.故当 m=3时,点Q到直线l的距离等于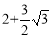 ;
;
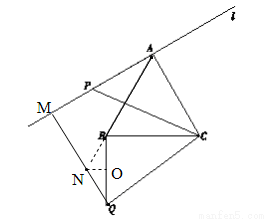
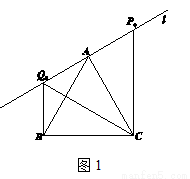
(2)所画图形如图.∵∠BAC=60°,∠CAQ0=90°,∴∠Q0AB=30°,同理可得:∠Q0BA=30°,∴Q0B= Q0A= P0A=m,在△Q0BC和△Q0AC中,∵ Q0B=Q0A,Q0C=Q0C,BC=AC,∴△Q0BC≌△Q0AC,∴∠Q0CB=∠Q0CA=30°,∵BC=4,∴Q0B=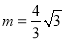 ;
;
(3)作BG⊥AC于点G,过点Q作直线l的垂线交l于点D,交BG于点F,∵ CA⊥直线l,∴ ∠CAP=90 ,易证四边形ADFG为矩形,∵ 等边三角形ABC的边长为4,∴ ∠ACB=60
,易证四边形ADFG为矩形,∵ 等边三角形ABC的边长为4,∴ ∠ACB=60 ,DF=AG=CG=
,DF=AG=CG=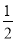 AC=2,∠CBG=
AC=2,∠CBG=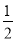 ∠CBA=30°,∵ 将△ACP绕点C按逆时针方向旋转60°得到△BCQ,∴ △ACP≌△BCQ.∴ AP = BQ = m,∠PAC=∠QBC=90
∠CBA=30°,∵ 将△ACP绕点C按逆时针方向旋转60°得到△BCQ,∴ △ACP≌△BCQ.∴ AP = BQ = m,∠PAC=∠QBC=90 .∴ ∠QBF=60
.∴ ∠QBF=60 .在Rt△QBF中,∠QFB=90
.在Rt△QBF中,∠QFB=90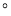 ,∠QBF=60
,∠QBF=60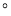 ,BQ=m,∴ QF=
,BQ=m,∴ QF=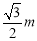 ,
,
要使△PAQ存在,则点P不能与点A,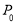 重合,所以点P的位置分为以下两种情况:
重合,所以点P的位置分为以下两种情况:
①如图2,当点P在(2)中的线段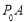 上(点P不与点A,
上(点P不与点A,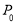 重合)时,可得
重合)时,可得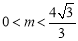 ,此时点Q在直线l的下方.∴ DQ=DF-QF=
,此时点Q在直线l的下方.∴ DQ=DF-QF=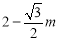 .∵
.∵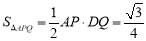 ,∴
,∴ 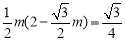 .整理,得
.整理,得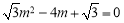 .解得
.解得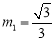 或
或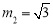 .经检验,
.经检验,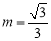 或
或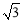 在
在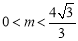 的范围内,均符合题意;
的范围内,均符合题意;
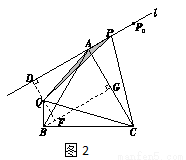
②如图3,当点P在(2)中的线段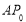 的延长线上(点P不与点A,
的延长线上(点P不与点A,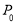 重合)时,可得
重合)时,可得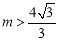 ,此时点Q在直线l的上方.∴DQ=QF-DF=
,此时点Q在直线l的上方.∴DQ=QF-DF= 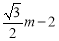 .∵
.∵ 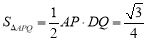 ,∴
,∴ 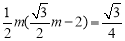 .整理,得
.整理,得 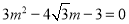 .解得
.解得 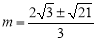 (舍负).经检验,
(舍负).经检验, 在
在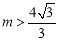 的范围内,符合题意.
的范围内,符合题意.
综上所述,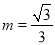 或
或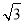 或
或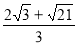 时,△PAQ的面积等于
时,△PAQ的面积等于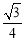 .
.

考点:1.等边三角形的性质;2.全等三角形的判定与性质;3.旋转的性质.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源:2014-2015学年河南省郑州市九年级第一次质量预测数学试卷(解析版) 题型:解答题
(10分)某旅馆有客房120间,每间房的日租金为160元,每天都客满.旅馆装修后要提高租金,经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?比装修前日租金的总收入增加多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省石家庄市九年级上学期第二次月考数学试卷(解析版) 题型:选择题
一元二次方程x(x-1)=0的解是( )
A.x=0 B.x=1 C.x=0或x=1 D.x=0或x=-1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市延庆县九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
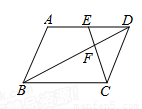
A.1:1 B.1:2 C.1:3 D.2:3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东400米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?(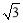 取1.732,结果精确到1米)
取1.732,结果精确到1米)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中, ,
,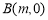 (其中
(其中 ),点P在以点
),点P在以点 为圆心,半径等于2的圆上,如果动点P满足∠APB=90°,
为圆心,半径等于2的圆上,如果动点P满足∠APB=90°,

(1)线段 的长等于 (用含m的代数式表示);(2)m的最小值为 .
的长等于 (用含m的代数式表示);(2)m的最小值为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省心学校九年级上学期数学试卷(解析版) 题型:解答题
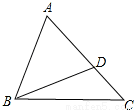
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com