
分析 首先计算乘方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
解答 解:($\frac{1}{4}$)-1+|1-$\sqrt{3}$|-3tan30°-(-2017)0
=4+$\sqrt{3}$-1-3×$\frac{\sqrt{3}}{3}$-1
=4+$\sqrt{3}$-1-$\sqrt{3}$-1
=2
故答案为:2.
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
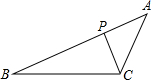 如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:∠ACP=∠B(或$\frac{AP}{AC}$=$\frac{AC}{AB}$)(写出一个即可).
如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:∠ACP=∠B(或$\frac{AP}{AC}$=$\frac{AC}{AB}$)(写出一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
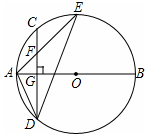 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 路程(千米) | 运费(元/吨•千米) | |||
| 甲库 | 乙库 | 甲库 | 乙库 | |
| A地 | 20 | 15 | 12 | 12 |
| B地 | 25 | 20 | 10 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com