
����Ŀ����һ���ϱ�����Ĺ�·�ϣ���һ�����ͣ��A�أ��˳��ĵ�һλ����������3ǧ���³����ó��������Ͽ���������2ǧ�������ڶ�λ���ˣ��ڶ�λ���˳˳�����7ǧ���³�����ʱǡ���е���λ�����ϳ���������3ǧ�ף��ֵ�ͷ�����ߣ�����³�ʱ���ǡ�õ���A�أ�
��1�������A��Ϊԭ�㣬����Ϊ��������1����λ��ʾ1ǧ�ף��������ϱ�ʾ����һλ���˺͵ڶ�λ�����³���λ�ã�
��2������λ���˳˳����˶���ǧ�ף�
��3���涨������շѱ���4ǧ���ڸ�7Ԫ������4ǧ�IJ���ÿǧ�Ӹ�1Ԫ������1ǧ�װ�1ǧ���㣩����ô�ó��˾��������λ�����й����˶���Ǯ��
���𰸡�(1) ��һλ�����ڵ�B���³����ڶ�λ�����ڵ�C���³�;(2) ����λ���˳˳�����8ǧ��;(3) �ó��˾��������λ�����й�����28Ԫ.
��������
��1�����������������ϱ�ʾ����һλ�����³��ĵص�B���ڶ�λ�����³��ĵص�C���ɣ�
��2�����������ʽ��Ȼ������������ļӼ����������м��㼴�ɣ�
��3������·�̷ֱ�������λ���˵�֧��Ǯ�����ٸ����������ļӷ����㷨����м��㼴����⣮
��1����ͼ��ʾ��
![]()
��һλ�����ڵ�B���³����ڶ�λ�����ڵ�C���³���
��2��3+��2+3��=3+5=8ǧ�ף�
�𣺵���λ���˳˳�����8ǧ�ף�
��3����һλ���˹���3ǧ�ף���7Ԫ��
�ڶ�λ���˹���7ǧ�ף���7+1����7-4��=7+3=10Ԫ��
����λ���˹���8ǧ�ף���7+1����8-4��=11Ԫ��
7+10+11=28Ԫ��
��ó��˾��������λ�����й�����28Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB�ϵ�һ�㣬��COD��ֱ�ǣ�OEƽ�֡�BOC��
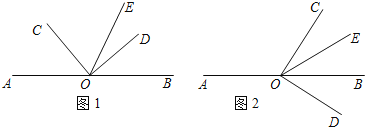
��1����ͼ��1��������AOC=![]() �����DOE�Ķ�����
�����DOE�Ķ�����
��2����ͼ��2��������COD�ƶ���O��ת���ұ�������OC��ֱ��AB�Ϸ�����������ת�����У�����AOC�Ķ����Ƕ���ʱ����COE=2��DOB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�͡�ADE���й�������ĵ���ֱ�������Σ���BAC=��DAE=90�㣬��PΪ����BD��CE�Ľ��㣮
��1����֤��BD=CE��
��2����AB=2��AD=1���ѡ�ADE�Ƶ�A��ת��
�ٵ���EAC=90��ʱ����PB�ij���
��ֱ��д����ת�������߶�PB������Сֵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ������ְ���μ��շ�֪ʶ���������ɼ��Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ������ͼ���ṩ����Ϣ����Щְ���ɼ�����λ����ƽ�����ֱ��ǣ� �� 
A.94�֣�96��
B.96�֣�96��
C.94�֣�96.4��
D.96�֣�96.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
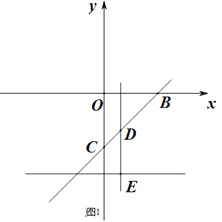
����Ŀ����֪��C(0,-2)��ֱ��l:y=kx-2k����kȡ��ֵ��ֱ���ܹ�����B��
(1)��B������.
(2)��ͼ1������DΪֱ��BC�ϣ���(-1,-3)���⣩һ����,����D��x��Ĵ��߽�y= - 3�ڵ�E����F��ֱ��BC�ϣ�����D��Ϊ![]() ����λ��D�������Ϊt����DEF�����ΪS����S��t������ϵʽ.
����λ��D�������Ϊt����DEF�����ΪS����S��t������ϵʽ.
(3)��ֱ��BC����x��Գƺ�������ƽ��5����λ�õ�ֱ��B1C1����ͼ2����G(1��a)��H(6,b)��ֱ��B1C1�����㣬��P(m,n)Ϊ��һ�����ڣ�G��H������⣩��һ�㣬,��mn=6��ֱ��PG��PHΪ�ֱ�y���ڵ�MN���㣬���߶�OM��ON��ʲô������ϵ����֤��.
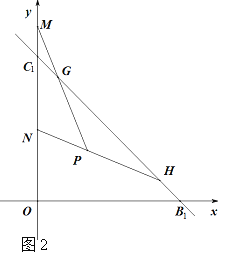
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���⻪ũ������˾����50̨�����ո�������м���20̨������30̨���Ƚ���50̨�����ո������A��B�������ո�С������30̨����A������20̨����B���������������ũ������˾�̶���ÿ������۸������
ÿ̨�����ո������� | ÿ̨�����ո������� | |
A���� | 1800 | 1600 |
B���� | 1600 | 1200 |
��1��������A����x̨���������ո��������˾��50̨�����ո��һ���õ����Ϊy��Ԫ������y��x��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2����ʹũ������˾��50̨�����ո��һ���õ�����ܶ����79 600Ԫ��˵���ж����ַ��䷽�����������ַ�����Ƴ�����
��3�����Ҫʹ��50̨�����ո��ÿ���õ������ߣ�����Ϊ�⻪ũ������˾��һ�����������飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
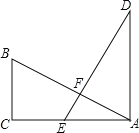
����Ŀ��(����7��)��ͼ����Rt��ABC������ACB=90�㣬EΪAC��һ�㣬��AE=BC������A��AD��CA������ΪA����AD=AC��AB��DE���ڵ�F.
��1���ж��߶�AB��DE��������ϵ��λ�ù�ϵ����˵�����ɣ�
��2������BD��BE������BC=a��AC=b��AB=c���������ı���ADBE�����֤�����ɶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�D��BC���ϵ�һ�㣬E��AD���е㣬��A����BC��ƽ���ߣ���CE���ӳ����ڵ�F����AF=BD������BF��
��1����֤��BD=CD����2�����AB=AC�����ж��ı���AFBD����״����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com