
【题目】我们知道,正整数的和1+3+5+…+(2n﹣1)=n2,若把所有正偶数从小到大排列,并按如下规律分组:(2),(4,6,8),(10,12,14,16,18),(20,22,24,26,28,30,32),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A8=(2,3),则A2018=_____
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,函数![]() 的图象经过
的图象经过![]() ,
,![]() ,其中
,其中![]() ,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.
,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.

(1)若![]() 的面积为4,求点B的坐标;
的面积为4,求点B的坐标;
(2)四边形ABCD能否成为平行四边形,若能,求点B的坐标,若不能说明理由;
(3)当![]() 时,求证:四边形ABCD是等腰梯形.
时,求证:四边形ABCD是等腰梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y=x2﹣1(﹣1≤x≤1)与x轴交于A、B两点,抛物线C2与抛物线C1关于点A中心对称,抛物线C3与抛物线C1关于点B中心对称.若直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点,则b的取值或取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高公民社会责任感,保证每个纳税人公平纳税,调节不同阶层贫富差距,营造“纳税光荣”社会氛围,2019年我国实行新的《个人收入所得税征收办法》,将个人收所得税的起征点提高至5000元(即全月个人收所得不超过5000元的,免征个人收入所得税):个人收入超过5000元的,其超出部分称为“应纳税所得额”,国家对纳税人的“应纳税所得额”实行“七级超额累进个人所得税制度”,该制度的前两级纳税标准如下:
①全月应纳税所得额不超过3000元的,按3%的税率计税;
②全月应纳税所得额超过3000元但不超过12000元的部分,按10%的税率计税.
按照新的《个人收入所得税征收办法》,在2019年某月,如果纳税人甲缴纳个人收入所得税75元,纳税人乙当月收入为9500元,纳税人丙缴纳个人收入所得税110元.
(1)甲当月个人收入所得是多少?
(2)乙当月应缴纳多少个人收入所得税?
(3)丙当月个人收入所得是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 共顶点
共顶点![]() ,
,![]() 和
和![]() 重合,
重合,![]() 为
为![]() 的平分线,
的平分线,![]() 为
为![]() 的平分线,
的平分线,![]() ,
,![]() .
.




(1)如图2,若![]() ,
,![]() ,则
,则![]()
(2)如图3,若![]() 绕
绕![]() 逆时针旋转,且
逆时针旋转,且![]() ,求
,求![]() .
.
(3)如图4,若![]() ,
,![]() 绕
绕![]() 逆时针旋转,转速为
逆时针旋转,转速为![]() /秒,同时
/秒,同时![]() 绕
绕![]() 逆时针旋转,转速为
逆时针旋转,转速为![]() /秒(转到
/秒(转到![]() 与
与![]() 共线时停止运动),且
共线时停止运动),且![]() 平分
平分![]() ,以下两个结论:①
,以下两个结论:① ![]() 为定值;②
为定值;②![]() 为定值,请选择正确的结论,并说明理由.
为定值,请选择正确的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3为边长作等边△A3A2B3,…,则等边△A2017A2018B2018的边长是_____.
与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3为边长作等边△A3A2B3,…,则等边△A2017A2018B2018的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
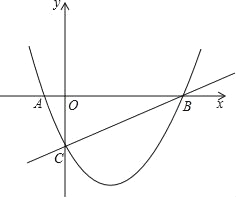
【题目】如图,已知抛物线y=ax2﹣![]() x+c与x轴相交于A、B两点,并与直线y=
x+c与x轴相交于A、B两点,并与直线y=![]() x﹣2交于B、C两点,其中点C是直线y=
x﹣2交于B、C两点,其中点C是直线y=![]() x﹣2与y轴的交点,连接AC.
x﹣2与y轴的交点,连接AC.
(1)求抛物线的解析式;
(2)证明:△ABC为直角三角形;
(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com