
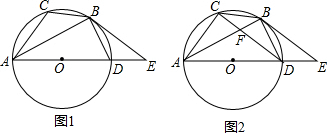
分析 (1)①连接OB,由条件可求得∠EBD=∠ABO,再利用圆周角定理可求得∠EBD+∠OBD=90°,可证明BE是⊙O的切线;
②利用圆内接四边形的性质可求得∠BDE=∠ACB,可证明△ACB∽△BDE,利用相似三角形的性质可求得DE的长;
(2)延长DB、AC交于点H,可证得△ABD≌△ABH,可求得HB,再利用△DCH∽△DBF,可求得DF的长,设⊙O的半径为r,则AD=AH=2r,在Rt△DCH中可求得CH=4,在Rt△ADC中,AD=2r,CD=8,AC=2r-4,由勾股定理可得到关于r的方程,可求得圆的半径.
解答 解:
(1)①如图1,连接OB,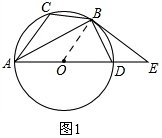
∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是⊙O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在⊙O上,
∴BE是⊙O的切线;
②∵四边形ACBD是圆的内接四边形,
∴∠ACB=∠BDE,且∠EBD=∠CAB,
∴△ACB∽△BDE,
∴$\frac{AC}{BD}$=$\frac{BC}{DE}$,即$\frac{6}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{DE}$,
解得DE=$\frac{10}{3}$;
(2)如图2,延长DB、AC交于点H,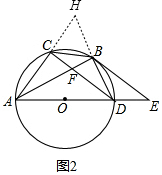
∵AD为⊙O的直径,
∴∠ABD=∠ABH=90°,
∵BD=BC,
∴∠DAB=∠HAB,
在△ABD和△ABH中
$\left\{\begin{array}{l}{∠DAB=∠HAB}\\{AB=AB}\\{∠ABD=∠ABH}\end{array}\right.$
∴△ABD≌△ABH(ASA),
∴BD=HB=2$\sqrt{5}$,
∵∠DCH=∠FBD=90°,
∴△DCH∽△DBF,
∴$\frac{DC}{BD}$=$\frac{DH}{DF}$,即$\frac{DF+3}{2\sqrt{5}}$=$\frac{4\sqrt{5}}{DF}$,解得DF=5,
设⊙O的半径为r,则AD=AH=2r,
在Rt△DCH中,CH=$\sqrt{D{H}^{2}-C{D}^{2}}$=$\sqrt{(4\sqrt{5})^{2}-{8}^{2}}$=4,
∴AC=2r-4,
在Rt△ACD中,由勾股定理可得AD2=AC2+CD2,
∴(2r)2=(2r-4)2+82,解得r=5,
即⊙O的半径为5.
点评 本题为圆的综合应用,涉及切线的判定和性质、相似三角形的判定和性质、圆圆角定理、全等三角形的判定和性质、方程思想等知识.在(1)②中证明△ACB∽△BDE是解题的关键,在(2)中构造三角形全等求得DF的长是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:填空题
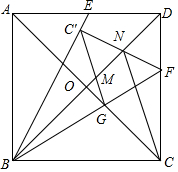 在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是6-$\frac{6}{5}\sqrt{5}$.
在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是6-$\frac{6}{5}\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
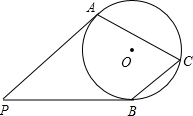 如图,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上,且$\widehat{ACB}$是优弧,则∠ACB等于( )
如图,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上,且$\widehat{ACB}$是优弧,则∠ACB等于( )| A. | 180°-2∠P | B. | 180°-∠P | C. | 90°-$\frac{1}{2}$∠P | D. | ∠P |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠B=2∠C | B. | ∠A+∠B=∠C | C. | ∠A:∠B:∠C=1:4:5 | D. | ∠A=37°,∠B=53° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
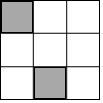 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )
如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )| A. | $\frac{5}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com