
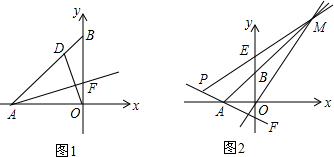
分析 (1)首先根据a2+b2-4a-4b=-8,可得(a-2)2+(b-2)2=0,据此求出a、b的值是多少;然后根据直角三角形的面积的求法,求出△ABO的面积是多少即可;
(2)首先求出直线AB的解析式,以及点F的坐标,进而求出直线AF的解析式;然后根据OD⊥AF,求出OD的斜率和OD的解析式;然后联立OD、AB的解析式,求出点D的坐标是多少即可;
(3)首先设BE=OF=a(m>0),求出AF、OM的解析式各为多少;然后联立AB、OM的解析式,求出点M的坐标,再根据点E的坐标是(0,2+a),确定出直线ME的解析式是多少;最后联立AF、ME的解析式,求出点P的坐标是多少;再判断出点P在EF的中垂线上,所以$\frac{PE}{PF}$=1,$\frac{PE}{PF}$的值一定,不发生变化,据此解答即可.
解答 解:(1)∵a2+b2-4a-4b=-8,
∴(a-2)2+(b-2)2=0,
∴a-2=0,b-2=0,
解得a=2,b=2,
∴S△ABO=$\frac{1}{2}$×|OA|×|OB|
=$\frac{1}{2}×2×2$
=2
(2)∵a=2,b=2,
∴A(-2,0),B(0,2),
∴直线AB的解析式为y=x+2;
∵直线y=$\frac{2}{3}$x+$\frac{4}{3}$交y轴于点F,
∴点F的坐标是:(0,$\frac{4}{3}$),
设直线AF的解析式是y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=0}\\{b=\frac{4}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
∴直线AF的解析式是y=$\frac{2}{3}$x+$\frac{4}{3}$,
∵OD⊥AF,
∴OD的斜率是:(-1)÷$\frac{2}{3}$=-$\frac{3}{2}$,
∴OD是解析式是y=-$\frac{3}{2}$x,
联立$\left\{\begin{array}{l}{y=-\frac{3}{2}x}\\{y=x+2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{4}{5}}\\{y=\frac{6}{5}}\end{array}\right.$,
∴点D的坐标是(-$\frac{4}{5}$,$\frac{6}{5}$).
(3)设BE=OF=a(a>0),
则E(0,2+a)、F(0,-a),
∵A(-2,0)、F(0,-a),
∴直线AF的解析式为:y=-$\frac{a}{2}$x-a;
∵OM⊥AF,
∴OM的斜率是:
(-1)÷(-$\frac{a}{2}$)=$\frac{2}{a}$,
∴OM的解析式为y=$\frac{2}{a}$x,
联立$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{2}{a}x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2a}{2-a}}\\{y=\frac{4}{2-a}}\end{array}\right.$,
∴点M的坐标是($\frac{2a}{2-a},\frac{4}{2-a}$),点E的坐标是(0,2+a),
∴设直线ME的解析式是:y=kx+b,
则$\left\{\begin{array}{l}{\frac{2a}{2-a}•k+b=\frac{4}{2-a}}\\{b=2+a}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{a}{2}}\\{b=2+a}\end{array}\right.$,
∴ME的解析式为y=$\frac{a}{2}$x+2+a,
联立$\left\{\begin{array}{l}{y=\frac{a}{2}x+2+a}\\{y=-\frac{a}{2}x-a}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-2-\frac{2}{a}}\\{y=1}\end{array}\right.$,
∴点P的坐标是(-2-$\frac{2}{a}$,1 ),
∵E(0,2+a)、F(0,-a),
∴EF的中垂线上点的纵坐标是:
(2+a-a)÷2
=2÷2
=1,
∵点P的纵坐标是1,
∴点P在EF的中垂线上,
∴PE=PF,
∴$\frac{PE}{PF}$=1,即$\frac{PE}{PF}$的值一定,不发生变化.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了三角形的面积的求法,直线解析式的求法,以及直线的中垂线的特征,要熟练掌握.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:选择题
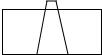 如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是( )
如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是( )| A. | 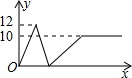 | B. | 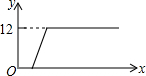 | C. | 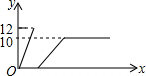 | D. | 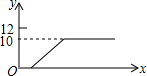 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
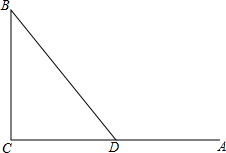 如图,A、B、C三个地点(图中的线段均是道路),AC⊥BC,甲、乙两人同时从A地出发,已知甲的速度比乙的速度快$\frac{1}{4}$,如果经C地到达B地,且使乙比甲早到B地,这是一个不可能的情况,但在距A地200米的D处有一条路可直通B地(即图中BD).
如图,A、B、C三个地点(图中的线段均是道路),AC⊥BC,甲、乙两人同时从A地出发,已知甲的速度比乙的速度快$\frac{1}{4}$,如果经C地到达B地,且使乙比甲早到B地,这是一个不可能的情况,但在距A地200米的D处有一条路可直通B地(即图中BD).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A(-3,0)和B(1,0),直线y=kx-4经过点A并且与y轴交于点C
如图,已知点A(-3,0)和B(1,0),直线y=kx-4经过点A并且与y轴交于点C查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com