
分析 (1)首先计算特殊角的三角函数值,计算0次幂、负指数次幂、去掉绝对值符号,然后进行加减计算即可;
(2)把第一个分式进行化简,对括号内的式子通分相减,然后把除法转化为乘法,计算乘法即可化简,最后代入数值计算即可.
解答 解:(1)原式=2$\sqrt{2}$•$\frac{\sqrt{2}}{2}$-1-($\sqrt{2}$-1)+4
=2-1-$\sqrt{2}$+1+4
=6-$\sqrt{2}$;
(2)原式=$\frac{(x-1)^{2}}{(x+1)(x-1)}$÷$\frac{x+1-3}{x+1}$
=$\frac{x-1}{x+1}$•$\frac{x+1}{x-2}$
=$\frac{x-1}{x-2}$.
当x=0时,原式=$\frac{-1}{-2}$=$\frac{1}{2}$.
点评 本题考查了实数的混合运算以及分式的化简求值,正确对分式进行通分、约分是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
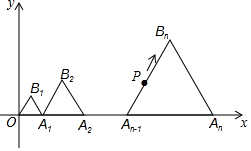 如图,在平面直角坐标系中,点A1,A2…,An都在x轴的正半轴上,OA1=1,A1A2=2,…An-1 An=n,分别以OA1,A1A2,…An-1 An为边,在x轴上方作等边三角形△OA1B1,△A1A2B2,…△An-1 AnBn,点B1,B2,…,Bn均落在第一象限,现有一动点P从点O出发,以每秒1个单位的速度沿折线O→B1→A1→B2→A2→…→Bn→An运动,则经2017秒后点P的坐标是(1008.5,$\frac{37\sqrt{3}}{2}$).
如图,在平面直角坐标系中,点A1,A2…,An都在x轴的正半轴上,OA1=1,A1A2=2,…An-1 An=n,分别以OA1,A1A2,…An-1 An为边,在x轴上方作等边三角形△OA1B1,△A1A2B2,…△An-1 AnBn,点B1,B2,…,Bn均落在第一象限,现有一动点P从点O出发,以每秒1个单位的速度沿折线O→B1→A1→B2→A2→…→Bn→An运动,则经2017秒后点P的坐标是(1008.5,$\frac{37\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
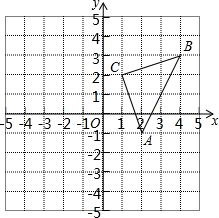 如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,
如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
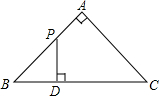 如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC的边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则y与x函数关系的图象大致是( )
如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC的边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则y与x函数关系的图象大致是( )| A. | 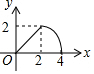 | B. | 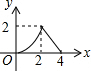 | C. | 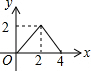 | D. | 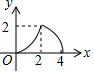 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com