
【题目】综合与探究:
如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣4=0,解得x1=﹣2,x2=8,
x﹣4=0,解得x1=﹣2,x2=8,
∵点B在点A的右侧,
∴点A的坐标为(﹣2,0),点B的坐标为(8,0).
当x=0时,y=﹣4,
∴点C的坐标为(0,﹣4).
(2)解:由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则
![]() ,
,
解得k=﹣ ![]() ,b=4.
,b=4.
∴直线BD的解析式为y=﹣ ![]() x+4.
x+4.
∵l⊥x轴,
∴点M的坐标为(m,﹣ ![]() m+4),点Q的坐标为(m,
m+4),点Q的坐标为(m, ![]() m2﹣
m2﹣ ![]() m﹣4).
m﹣4).
如图,当MQ=DC时,四边形CQMD是平行四边形,

∴(﹣ ![]() m+4)﹣(
m+4)﹣( ![]() m2﹣
m2﹣ ![]() m﹣4)=4﹣(﹣4).
m﹣4)=4﹣(﹣4).
化简得:m2﹣4m=0,
解得m1=0(不合题意舍去),m2=4.
∴当m=4时,四边形CQMD是平行四边形.
此时,四边形CQBM是平行四边形.
解法一:∵m=4,
∴点P是OB的中点.
∵l⊥x轴,
∴l∥y轴,
∴△BPM∽△BOD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BM=DM,
∵四边形CQMD是平行四边形,
∴DM ![]() CQ,
CQ,
∴BM ![]() CQ,
CQ,
∴四边形CQBM是平行四边形.
解法二:设直线BC的解析式为y=k1x+b1,则
![]() ,
,
解得k1= ![]() ,b1=﹣4.
,b1=﹣4.
故直线BC的解析式为y= ![]() x﹣4.
x﹣4.
又∵l⊥x轴交BC于点N,
∴x=4时,y=﹣2,
∴点N的坐标为(4,﹣2),
由上面可知,点M的坐标为(4,2),点Q的坐标为(4,﹣6).
∴MN=2﹣(﹣2)=4,NQ=﹣2﹣(﹣6)=4,
∴MN=QN,
又∵四边形CQMD是平行四边形,
∴DB∥CQ,
∴∠3=∠4,
∵在△BMN与△CQN中,
 ,
,
∴△BMN≌△CQN(ASA)
∴BN=CN,
∴四边形CQBM是平行四边形.
(3)解:抛物线上存在两个这样的点Q,分别是Q1(﹣2,0),Q2(6,﹣4).
若△BDQ为直角三角形,可能有三种情形,如答图2所示:
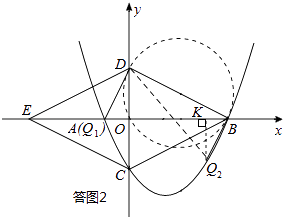
①以点Q为直角顶点.
此时以BD为直径作圆,圆与抛物线的交点,即为所求之Q点.
∵P在线段EB上运动,
∴﹣8≤xQ≤8,而由图形可见,在此范围内,圆与抛物线并无交点,
故此种情形不存在.
②以点D为直角顶点.
连接AD,∵OA=2,OD=4,OB=8,AB=10,
由勾股定理得:AD= ![]() ,BD=
,BD= ![]() ,
,
∵AD2+BD2=AB2,
∴△ABD为直角三角形,即点A为所求的点Q.
∴Q1(﹣2,0);
③以点B为直角顶点.
如图,设Q2点坐标为(x,y),过点Q2作Q2K⊥x轴于点K,则Q2K=﹣y,OK=x,BK=8﹣x.
易证△Q2KB∽△BOD,
∴ ![]() ,即
,即 ![]() ,整理得:y=2x﹣16.
,整理得:y=2x﹣16.
∵点Q在抛物线上,∴y= ![]() x2﹣
x2﹣ ![]() x﹣4.
x﹣4.
∴ ![]() x2﹣
x2﹣ ![]() x﹣4=2x﹣16,解得x=6或x=8,
x﹣4=2x﹣16,解得x=6或x=8,
当x=8时,点Q2与点B重合,故舍去;
当x=6时,y=﹣4,
∴Q2(6,﹣4).
综上所述,符合题意的点Q的坐标为(﹣2,0)或(6,﹣4)
【解析】(1)根据函数解析式,求出当x=0和y=0是的函数值、自变量的值,即可求出点A、B、C三点坐标。
(2)先根据菱形是轴对称图形求出点D的坐标,在利用待定系数法求出直线DB的函数解析式,再分别表示出点M的坐标点Q的坐标,根据平行四边形的性质,得出关于m的方程即可求出m的值,即可判断四边形CQBM是平行四边形。
(3)要使△BDQ为直角三角形,分三种情况:①以点Q为直角顶点;②以点D为直角顶点;③以点B为直角顶点.根据勾股定理和相似三角形的判定和性质,分别求出点Q的坐标即可。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握平行四边形的判定与性质(若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积)的相关知识才是答题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为了参加学校举办的“新城杯”足球联赛,新城中学七(1)班学生去商场购买了A品牌足球1个、B品牌足球2个,共花费400元,七(2)班学生购买了品牌A足球3个、B品牌足球1个,共花费450元.
(1)求购买一个A种品牌、一个B种品牌的足球各需多少元?
(2)为了进一步发展“校园足球”,学校准备再次购进A、B两种品牌的足球,学校提供专项经费850元全部用于购买这两种品牌的足球,学校这次最多能购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1=a(x﹣2)2+c(a≠0)的图象与y轴的交点为(0,1),在x轴上截得的线段长为 ![]() .
.
(1)求a、c的值.
(2)对于任意实数k,规定:当﹣2≤x≤1时,关于x的函数y2=y1﹣kx的最小值称为k的“贡献值”,记作g(k).求g(k)的解析式.
(3)在(2)条件下,当“贡献值”g(k)=1时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: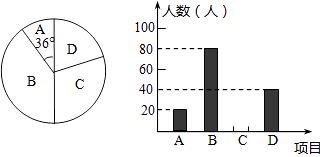
(1)这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一小长假的某一天,亮亮全家上午![]() 时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )

A.景点离亮亮的家![]() 千米
千米
B.亮亮到家的时间为![]() 时
时
C.小汽车返程的速度为![]() 千米/时
千米/时
D.![]() 时至
时至![]() 时,小汽车匀速行驶
时,小汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.
(1)求∠BPC的度数.
(2)求该铁塔PF的高度,(结果精确到0.1m,参考数据: ![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是线段AB上一点,AC和DG相交于点E.
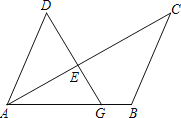
(1)请先作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
(2)然后证明当:AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com