
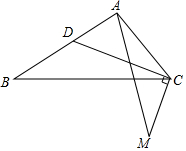
 如图,△ABC中,∠ACB=α(0°<α<90°),CD平分∠ACB,过C点作CD的垂线交AB的垂直平分线于M,连接AM,求∠BAM(用含α的式子表示).
如图,△ABC中,∠ACB=α(0°<α<90°),CD平分∠ACB,过C点作CD的垂线交AB的垂直平分线于M,连接AM,求∠BAM(用含α的式子表示). 分析 先连接BM,过M作MQ⊥AB于H,交CD的延长线于Q,连接AQ,BQ,根据MQ即为AB的垂直平分线,得出AQ=BQ,再过Q作QE⊥CA于E,作QF⊥BC于F,判定Rt△AEQ≌Rt△BFQ(HL),得出A,Q,B,C四点共圆,再根据∠QCM=90°,得出M在△BQC的外接圆上,即A,C,M,B,Q五点共圆,最后根据MB=MA,求得∠BAM=90°-$\frac{1}{2}$α.
解答 解:连接BM,过M作MQ⊥AB于H,交CD的延长线于Q,连接AQ,BQ,
由题可得,M在AB的垂直平分线上,
∴MQ即为AB的垂直平分线,
∴AQ=BQ,
过Q作QE⊥CA于E,作QF⊥BC于F,
∵在四边形ACBQ中,CQ平分∠ACB,
∴QE=QF,
∴Rt△AEQ≌Rt△BFQ(HL),
∴∠QAE=∠QBF,
∵∠QAE+∠QAC=180°,
∴∠QBF+∠QAC=180°,
∴A,Q,B,C四点共圆,
∴QM垂直平分弦AB,圆心在QM上,
∵∠QCM=90°,
∴M在△BQC的外接圆上,
∴A,C,M,B,Q五点共圆,
∴∠AMB=∠ACB=α,
∵MB=MA,
∴∠BAM=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α.
点评 本题主要考查了线段垂直平分线的性质,全等三角形的判定与性质,等腰三角形的性质以及四点共圆的综合应用,解决问题的关键是作辅助线构造全等三角形和等腰三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
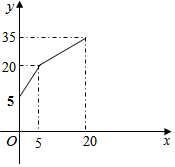 一个水槽有进水管和出水管各一个,进水管每分钟进水m升,出水管每分钟出水n升,水槽在开始5分钟内只进水不出水,随后15分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示:
一个水槽有进水管和出水管各一个,进水管每分钟进水m升,出水管每分钟出水n升,水槽在开始5分钟内只进水不出水,随后15分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
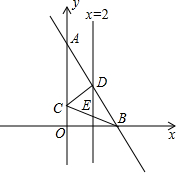 如图,平面直角坐标系中,直线AB:y=-2x+8交y轴于点A,交x轴于点B,以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上,连接BC,直线x=2交AB于点D,交BC于点E,交x轴于点G,连接CD.
如图,平面直角坐标系中,直线AB:y=-2x+8交y轴于点A,交x轴于点B,以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上,连接BC,直线x=2交AB于点D,交BC于点E,交x轴于点G,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在数轴上分别画出点A、B、C、D,点A表示数$\frac{1}{3}$,点B表示数1$\frac{1}{2}$,点C表示数-2,点D表示数2$\frac{3}{4}$;并将点A、B、C、D所表示的数用“>”连接.
在数轴上分别画出点A、B、C、D,点A表示数$\frac{1}{3}$,点B表示数1$\frac{1}{2}$,点C表示数-2,点D表示数2$\frac{3}{4}$;并将点A、B、C、D所表示的数用“>”连接.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com