①②④(每填对一个给1分,多选或错选不给分)
分析:由四边形ABCD为正方形,得到四条边相等,四个内角都为直角.由于△AED与△ECP都是直角三角形,根据如果两个三角形有两组对应边的比相等,并且它们的夹角也相等,则当PC:DE=EC:AD时能得到△AED与△ECP相似,即可得到BP=2CP.
解答:①∵四边形ABCD为正方形,

∴∠C=∠D=90°,
当∠AED=∠PEC时,又∠D=∠C=90°,
∴△AED∽△PEC;
故本选项正确;
②∵四边形ABCD为正方形,
∴∠C=∠D=90°,
当∠AEP=90°时,∠DAE=∠CEP(同角的余角相等).
又∠D=∠C=90°,
∴△AED∽△EPC;
故本选项正确;

当P是BC的中点时,PC=CE,则
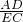
=2,
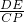
=1,
∴
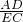
≠
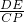
,
∴△AED与△ECP不相似.
故本选项错误;
④∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°.
若BP:BC=3:4时,设BP=3k,BC=4k.则AD=CD=BC=4k,CP=BC-BP=k,
∴CE=DE=2k,
∴
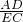
=

=2,
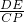
=
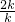
=2,
∴
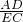
=
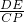
.
又∠D=∠C=90°,
∴△AED∽△ECP;
故本选项正确;
综上所述,可以推出△AED与△ECP相似的有:①②④.
故答案是:①②④.
点评:考查相似三角形的判定定理:
(1)两角对应相等的两个三角形相似.
(2)两边对应成比例且夹角相等的两个三角形相似.
(3)三边对应成比例的两个三角形相似.
(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.

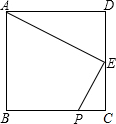 如图所示,已知四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,可以推出△AED与△ECP相似的有________.
如图所示,已知四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,可以推出△AED与△ECP相似的有________.

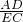 =2,
=2,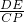 =1,
=1,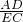 ≠
≠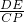 ,
,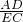 =
= =2,
=2,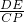 =
=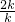 =2,
=2,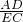 =
=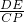 .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案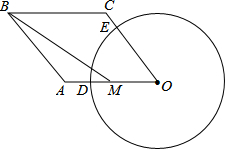 (2013•厦门)如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
(2013•厦门)如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
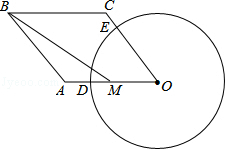 如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=