
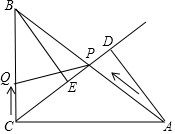
 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点P沿AB边从点A开始以2cm/s的速度向点B运动,点Q沿CB边从点C开始以1cm/s的速度向点B运动,P、Q同时出发,用t(s)表示运动的时间(0≤t≤5).
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点P沿AB边从点A开始以2cm/s的速度向点B运动,点Q沿CB边从点C开始以1cm/s的速度向点B运动,P、Q同时出发,用t(s)表示运动的时间(0≤t≤5).分析 (1)根据勾股定理得到BC=10,根据已知条件得到PA=2t,BP=10-2t,CQ=t,BQ=6-t.根据相似三角形的性质列方程即可得到结论;
(2)如图1,作PF⊥AC,垂足为F.根据相似三角形的性质得到PF=$\frac{6t}{5}$,AF=$\frac{8t}{5}$.求得CF=8-$\frac{8t}{5}$,根据勾股定理得到CP=$\sqrt{C{F}^{2}+P{F}^{2}}$=2$\sqrt{{t}^{2}-\frac{32}{5}t+16}$,根据三角形的面积即可得到结论;
(3)如图2,设PQ的中点为M,以C为原点,以AC所在直线为x轴,建立平面直角坐标系,依题意,可知0≤t≤5,当t=0时,点M1的坐标为(4,0);当t=5时,点M2的坐标为(0,5.5),求得直线M1M2的解析式为y=-$\frac{11}{8}$x+$\frac{11}{2}$.根据勾股定理即可得到结论.
解答  解:(1)∵∠ACB=90°,AC=8cm,BC=6cm,
解:(1)∵∠ACB=90°,AC=8cm,BC=6cm,
∴BC=10cm.
由题意可知,PA=2t,BP=10-2t,CQ=t,BQ=6-t.
①若$\frac{BQ}{BC}=\frac{BP}{BA}$,则△BQP∽△BCA.
即$\frac{6-t}{6}=\frac{10-2t}{10}$.解得t=0;
②若$\frac{BQ}{BA}=\frac{BP}{BC}$,则△BQP∽△BAC.
即$\frac{6-t}{10}=\frac{10-2t}{6}$.解得t=$\frac{32}{7}$.
故当t=0或t=$\frac{32}{7}$时,以P,Q,C为顶点的三角形与△ABC相似,
(2)如图1,作PF⊥AC,垂足为F.
∴△APF∽△ABC.
∴$\frac{AP}{AB}=\frac{PF}{BC}=\frac{AF}{AC}$,即$\frac{2t}{10}=\frac{PF}{6}=\frac{AF}{8}$,
解得PF=$\frac{6t}{5}$,AF=$\frac{8t}{5}$.
∴CF=8-$\frac{8t}{5}$,
∴CP=$\sqrt{C{F}^{2}+P{F}^{2}}$=2$\sqrt{{t}^{2}-\frac{32}{5}t+16}$,
∵S△APC=$\frac{1}{2}$CP•AD=$\frac{1}{2}$PF•AC=$\frac{1}{2}$•$\frac{6t}{5}$•8=$\frac{1}{2}$•$\frac{48t}{5}$,
∴AD=$\frac{48t}{5CP}$.
同理BE=$\frac{48-\frac{48t}{5}}{CP}$.
∴y=AD+BE=$\frac{48t}{5CP}$+$\frac{48-\frac{48t}{5}}{CP}$=$\frac{48}{CP}$=$\frac{24}{\sqrt{{t}^{2}-\frac{32}{5}t+16}}$,
y=$\frac{24}{\sqrt{{t}^{2}-\frac{32}{5}t+16}}$=$\frac{24}{\sqrt{(t-\frac{16}{5})^{2}+\frac{144}{25}}}$,当t=$\frac{16}{5}$时,y的最大值为10cm;
(3)如图2,设PQ的中点为M, 以C为原点,以AC所在直线为x轴,建立平面直角坐标系,
以C为原点,以AC所在直线为x轴,建立平面直角坐标系,
依题意,可知0≤t≤5,当t=0时,点M1的坐标为(4,0);
当t=5时,点M2的坐标为(0,5.5),设直线M1M2的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{4k+b=0}\\{b=5.5}\end{array}\right.$∴$\left\{\begin{array}{l}{k=-\frac{11}{8}}\\{b=\frac{11}{2}}\end{array}\right.$,
∴直线M1M2的解析式为y=-$\frac{11}{8}$x+$\frac{11}{2}$.
由(2)知点Q(0,t),P(8-$\frac{8t}{5}$,$\frac{6t}{5}$),
∴在运动过程中,线段PQ中点M3的坐标为(4-$\frac{4t}{5}$,$\frac{11t}{10}$),
把x=4-$\frac{4t}{5}$,代入y=-$\frac{11}{8}$x+$\frac{11}{2}$,得y=$\frac{11t}{10}$,
∴点M3在M1M2直线上,
∴线段PQ中点M所经过的路径长为$\sqrt{{4}^{2}+5.{5}^{2}}$=$\frac{\sqrt{185}}{2}$cm.
点评 本题考查了相似三角形的判定和性质,二次函数的最值问题,待定系数法求函数的解析式,勾股定理,正确的作出辅助线是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
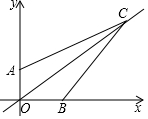 如图,已知点A(0,3),B(4,0),点C在第一象限,且AC=5$\sqrt{5}$,BC=10,则直线OC的函数表达式为y=$\frac{4}{5}$x.
如图,已知点A(0,3),B(4,0),点C在第一象限,且AC=5$\sqrt{5}$,BC=10,则直线OC的函数表达式为y=$\frac{4}{5}$x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
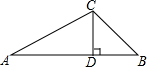 南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)
南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
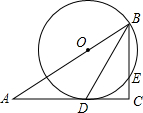 如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:| 兴趣班名称 | 频率 |
| “无人机” | a |
| “3D打印” | 0.05 |
| “网页设计” | 0.25 |
| “电脑绘画” | 0.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com