
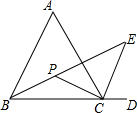
 如图所示,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线交于点P,延长BC到D,∠ACD的平分线交BP的延长线于点E,求∠BPC和∠E的度数.
如图所示,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线交于点P,延长BC到D,∠ACD的平分线交BP的延长线于点E,求∠BPC和∠E的度数. 分析 根据三角形内角和定理和角平分线的性质得到∠BPC=180°-$\frac{1}{2}$(∠ABC+∠ACB)=120°,所以∠EPC=60°,再由CE是∠ACD的平分线,可证∠BCP=90°,进而可求出∠E的度数.
解答 解:∵在△ABC中∠A=60°,
∴∠ABC+∠ACB=120°.
∵BE是∠ABC的角平分线,
∴∠PBC=$\frac{1}{2}$∠ABC.
又∵CP是∠ACB的平分线,
∴∠PCB=$\frac{1}{2}$∠ACB,
∴∠BPC=180°-∠PBC-∠PCB=180°-$\frac{1}{2}$(∠ABC+∠ACB)=120°,
∴∠EPC=60°,
∵CE是∠ACD的平分线,
∴∠BCP=$\frac{1}{2}$(∠BCA+∠ACD)=90°,
∴∠E=90°-60°=30°.
点评 本题考查三角形外角的性质及三角形的内角和定理,解题的关键是利用平角为180°以及角平分线的性质求得∠BCP=$\frac{1}{2}$(∠BCA+∠ACD)=90°.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | 14 | B. | 140 | C. | 1400 | D. | 14000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{ac}{{b}^{2}}$$\sqrt{abc}$ | B. | $\frac{ac}{{b}^{2}}$$\sqrt{-abc}$ | C. | -$\frac{ac}{{b}^{2}}$$\sqrt{-abc}$ | D. | -$\frac{ac}{{b}^{2}}$$\sqrt{abc}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
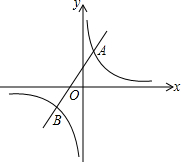 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com