
倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径。下面是一案例,请同学们认真阅读、研究,完成“类比猜想”及后面的问题。
习题解答:
习题 如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由。
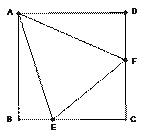
习题研究
 观察分析 观察图(1),由解答可知,该题有用的条件是①ABCD是四边形,点E、F分别在边BC、CD上;②AB=AD;③∠B=∠D=90°;
观察分析 观察图(1),由解答可知,该题有用的条件是①ABCD是四边形,点E、F分别在边BC、CD上;②AB=AD;③∠B=∠D=90°;
④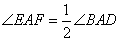 。答:成立。
。答:成立。
类比猜想
(1)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,
∠B=∠D,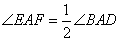 时,还有EF=BE+DF吗?答:不一定成立。
时,还有EF=BE+DF吗?答:不一定成立。
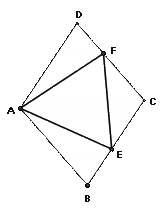
研究一个问题,常从特例入手,请同学们研究:如图(2),在菱
形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°
时,还有EF=BE+DF吗?
(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180,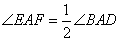 时,EF=BE+DF吗?
时,EF=BE+DF吗?
科目:初中数学 来源: 题型:
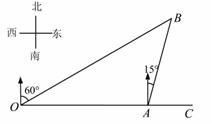
如图,港口A在观测站O的正东方向,OA=4km.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为
A.4km B.2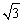 km C.2
km C.2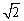 km D.(
km D.(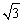 +1)km
+1)km
查看答案和解析>>
科目:初中数学 来源: 题型:
每天锻炼一小时,健康生活一辈子”,自开展“阳光体育运动”以来,学校师生的锻炼意识都增强了,某校有学生8200人,为 了解学生每
了解学生每 天的锻炼]
天的锻炼]
时间,学校体育组随机调查了部分学生,统计结果如
表所示。
表格中,m= ;
这组数据的众数是 ;
该校每天锻炼时间达到1小时的约有 人。
查看答案和解析>>
科目:初中数学 来源: 题型:
四张背面完全相同的纸牌(如图,用①、②、③、④表示)。正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后, 先随机抽出一张(不放回),再随机抽出一张。
先随机抽出一张(不放回),再随机抽出一张。

(1)、写出两次摸牌出现的所有可能的结果(用①、②、③、④表示);
(2)、以两次摸出的牌面上的结果为条件,求能判断四边形ABCD为平行四边形的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( )

|
| A. | 4个 | B. | 6个 | C. | 8个 | D. | 10个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某市6月份某周气温(单位:摄氏度)为23,25,28,25,28,31,28,则这组数据的众数和中位数分别是( )
A25 25 B2 8 28 C25 28 D28 31
8 28 C25 28 D28 31
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com