
分析 分子都是1,分母可以拆成连续两个自然数的乘积,奇数位置为负,偶数位置为正,由此规律得出第n个数为(-1)n$\frac{1}{n(n+1)}$,代入数值求得答案即可.
解答 解:∵第n个数为(-1)n$\frac{1}{n(n+1)}$,
∴第10个数是$\frac{1}{10×11}$=$\frac{1}{110}$,第15个数是-$\frac{1}{15×16}$=-$\frac{1}{240}$,第2006个数是$\frac{1}{2006×2007}$=$\frac{1}{4026042}$.
故答案为:$\frac{1}{110}$,-$\frac{1}{240}$,$\frac{1}{4206042}$.
点评 此题考查数字的变化规律,找出数字之间的联系,得出数字之间的运算规律,利用规律解决问题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD是菱形ABCD的对角线,点E是边BC上的动点,连接AE,点F在线段AE上,连接BF,DF,且∠AFB=60°,AB=BD
如图,BD是菱形ABCD的对角线,点E是边BC上的动点,连接AE,点F在线段AE上,连接BF,DF,且∠AFB=60°,AB=BD查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=2BC,E是AB上一点,O是CD上一点,以OC为半径作⊙O,将△ADE折叠至△A′DE,点A′在⊙O上,延长EA′交BC延长线于F,且恰好过点O,过点D作⊙O的切线交BC延长线于点G.若FG=1,则AD=2,⊙O半径=$\frac{3}{2}$.
如图,矩形ABCD中,AB=2BC,E是AB上一点,O是CD上一点,以OC为半径作⊙O,将△ADE折叠至△A′DE,点A′在⊙O上,延长EA′交BC延长线于F,且恰好过点O,过点D作⊙O的切线交BC延长线于点G.若FG=1,则AD=2,⊙O半径=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
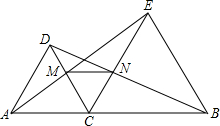 已知:如图,点C是线段AB上的动点(C点于A、B不重合),分别以AC、BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE于CD相交于点M,BD与CE相交于点N.
已知:如图,点C是线段AB上的动点(C点于A、B不重合),分别以AC、BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE于CD相交于点M,BD与CE相交于点N.| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com