
【题目】已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).
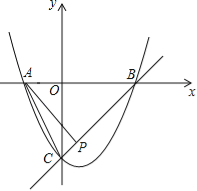
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式和∠ABC的度数;
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)45°;(3)P(![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)直接将A,C点坐标代入抛物线解析式求出即可;
(2)首先求出B点坐标,进而利用待定系数法求出直线BC的解析式,进而利用CO,BO的长求出∠ABC的度数;
(3)利用∠ACB=∠PAB,结合相似三角形的判定与性质得出BP的长,进而得出P点坐标.
解:(1)将点A的坐标(﹣1,0),点C的坐标(0,﹣3)代入抛物线解析式得:
![]() ,
,
解得:![]() ,
,
故抛物线解析式为:y=x2﹣2x﹣3;
(2)由(1)得:0=x2﹣2x﹣3,
解得:x1=﹣1,x2=3,故B点坐标为:(3,0),
设直线BC的解析式为:y=kx+d,
则![]() ,
,
解得:![]() ,
,
故直线BC的解析式为:y=x﹣3,
∵B(3,0),C(0,﹣3),
∴BO=OC=3,
∴∠ABC=45°;
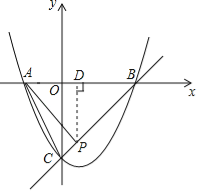
(3)过点P作PD⊥x轴于点D,
∵∠ACB=∠PAB,∠ABC=∠PBA,
∴△ABP∽△CBA,
∴![]() =
=![]() ,
,
∵BO=OC=3,
∴BC=3![]() ,
,
∵A(﹣1,0),B(3,0),
∴AB=4,
∴![]() =
=![]() ,
,
解得:BP=![]() ,
,
由题意可得:PD∥OC,
∴DB=DP=![]() ,
,
∴OD=3﹣![]() =
=![]() ,
,
则P(![]() ,﹣
,﹣![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与y轴交于点C,与![]() 轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
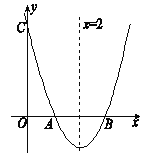
(1) 求抛物线的函数表达式;
(2) 如果抛物线的对称轴上存在一点P,使得△APC周长的最小,求此时△APC周长.
(3) 设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是菱形,求点D的坐标.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com