
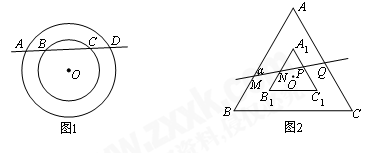
【初始问题】如图1,已知两个同心圆,直线AD分别交大⊙O于点A、D,交小⊙O于点B、C.AB与CD相等吗?请证明你的结论.
【类比研究】如图2,若两个等边三角形ABC和A1 B1 C1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,AC∥A1C1,可知AB与A1B1,BC与B1C1,AC与A1C1之间的距离相等.直线MQ分别交三角形的边于点M、N、P、Q,与AB所成夹角为∠α(30°<∠α<90°).
1.(1)求![]() (用含∠α的式子表示);
(用含∠α的式子表示);
2.(2)求∠α等于多少度时,MN = PQ.
1.解:【初始问题】结论:AB = CD. ……………………… 1分
证明:如图,作OE⊥AD于E.
∴ AE=ED,BE=EC. …………………………………………… 2分
∴ AE-BE=ED-EC.
即 AB=CD. ……………………………………………………… 3分
【类比研究】(1)如图,作ND⊥AB于D,PE⊥AC于E. ……… 4分
则 ND=PE.
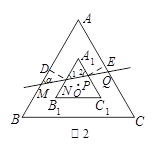 ∵ AB∥A1B1,
∵ AB∥A1B1,
∴ ∠1=∠α.
∵ 等边三角形A1 B1 C1中,∠A1=60°,
∴ ∠2=120°-∠1=120°-∠α.
∵ AC∥A1C1,
∴ ∠PQE=∠2=120°-∠α.
∵ 30°<∠α<90°,
∴ 30°<120°-∠α<90°.
∴ 在Rt△MDN和Rt△QEP中,
DN=MN![]() ,PE= PQ
,PE= PQ![]() . …………………… 6分
. …………………… 6分
∴MN![]() = PQ
= PQ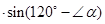 .
.
∴![]() .
.
2.(2)当120°-∠α =∠α时,即∠α = 60°时,MN=PQ.
解析:略


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

 (用含∠α的式子表示);
(用含∠α的式子表示);查看答案和解析>>
科目:初中数学 来源:2012届北京市西城区八年级上学期期末考试(A卷)数学卷 题型:解答题
有一个装有进水管和出水管的容器,水管的所有阀门都处于关闭状态.初始时,打开容器的进水管,只进水;到5分钟时,打开容器的出水管,此时既进水又出水;到15分钟时,关闭容器的进水管,只出水;到 分钟时,容器内的水全部排空.已知此容器每分钟的进水量与出水量均为常数,容器内的水量
分钟时,容器内的水全部排空.已知此容器每分钟的进水量与出水量均为常数,容器内的水量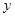 (单位:升)与时间
(单位:升)与时间 (单位:分)之间的函数关系如图所示,请根据图象回答下列问题:
(单位:分)之间的函数关系如图所示,请根据图象回答下列问题:
【小题1】(1)此容器的进水管每分钟进水______升;
【小题2】(2)求 时,容器内的水量
时,容器内的水量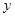 与时间
与时间 的函数关系式;
的函数关系式;
【小题3】(3)此容器的出水管每分钟出水多少升? 的值为多少?
的值为多少?
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京昌平区九年级第一学期期末考试数学卷 题型:解答题
【初始问题】如图1,已知两个同心圆,直线AD分别交大⊙O于点A、D,交小⊙O于点B、C.AB与CD相等吗?请证明你的结论.
【类比研究】如图2,若两个等边三角形ABC和A1 B1 C1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,AC∥A1C1,可知AB与A1B1,BC与B1C1,AC与A1C1之间的距离相等.直线MQ分别交三角形的边于点M、N、P、Q,与AB所成夹角为∠α(30°<∠α<90°).
【小题1】(1)求 (用含∠α的式子表示);
(用含∠α的式子表示);
【小题2】(2)求∠α等于多少度时,MN = PQ.
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京昌平区九年级第一学期期末考试数学卷 题型:解答题
【初始问题】如图1,已知两个同心圆,直线AD分别交大⊙O于点A、D,交小⊙O于点B、C.AB与CD相等吗?请证明你的结论.
【类比研究】如图2,若两个等边三角形ABC和A1 B1 C1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,AC∥A1C1,可知AB与A1B1,BC与B1C1,AC与A1C1之间的距离相等.直线MQ分别交三角形的边于点M、N、P、Q,与AB所成夹角为∠α(30°<∠α<90°).

1.(1)求 (用含∠α的式子表示);
(用含∠α的式子表示);
2.(2)求∠α等于多少度时,MN = PQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com