
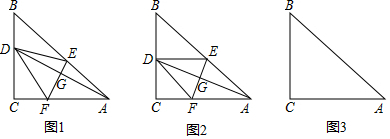
分析 (1)由折叠的性质得:EF⊥AD,DG=AG,DE=AE,DF=AF,由平行线的性质得出∠DEG=∠AFG,由AAS证明△DEG≌△AFG,得出DE=AF,证出四边形AEDF是平行四边形,即可得出结论;
(2)求出CD=BC-BD=2,设AF=DF=x,则CF=4-x,在Rt△CDF中,由勾股定理得出方程,解方程即可;
(3)设DF=AF=x,则CF=4-x,由折叠的性质得:△DFG的面积=△AFG的面积,当p=$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{16}$时,由三角形面积关系求出DF=$\frac{5}{2}$=2.5,CF=1.5,由勾股定理得出CD=2;当p=$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{3}$时,求出DF=$\frac{8}{3}$,CF=$\frac{4}{3}$,由勾股定理求出CD=$\frac{4\sqrt{3}}{3}$;即可得出答案.
解答 解:(1)当DE∥AC时,四边形AEDF是菱形;理由如下:
由折叠的性质得:EF⊥AD,DG=AG,DE=AE,DF=AF,
∵DE∥AC,
∴∠DEG=∠AFG,
在△DEG和△AFG中,$\left\{\begin{array}{l}{∠DEG=∠AFG}&{\;}\\{∠DGE=∠AGF}&{\;}\\{DG=AG}&{\;}\end{array}\right.$,
∴△DEG≌△AFG(AAS),
∴DE=AF,
∴四边形AEDF是平行四边形,
又∵DE=AE,
∴四边形AEDF是菱形;
(2)∵BD=1,
∴CD=BC-BD=2,
设AF=DF=x,则CF=4-x,
∵∠ACB=90°,
∴CD2+CF2=DF2,即22+(4-x)2=x2,
解得:x=2.5,
即AF的长为2.5;
(3)设DF=AF=x,则CF=4-x,
由折叠的性质得:△DFG的面积=△AFG的面积,
当p=$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{16}$时,$\frac{x}{4}$=$\frac{10}{16}$=$\frac{5}{8}$,
解得:x=2.5,
∴DF=$\frac{5}{2}$=2.5,CF=1.5,
∴CD=$\sqrt{D{F}^{2}-C{F}^{2}}$=$\sqrt{2.{5}^{2}-1.{5}^{2}}$=2;
当p=$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{3}$时,$\frac{x}{4}$=$\frac{2}{3}$,
解得:x=$\frac{8}{3}$,
∴DF=$\frac{8}{3}$,CF=$\frac{4}{3}$,
∴CD=$\sqrt{D{F}^{2}-C{F}^{2}}$=$\frac{4\sqrt{3}}{3}$;
∴当$\frac{5}{16}$≤p≤$\frac{1}{3}$时,CD的变化范围为$\frac{5}{2}$≤CD≤$\frac{4\sqrt{3}}{3}$.
点评 本题是四边形综合题目,考查了折叠的性质、全等三角形的判定与性质、平行四边形的判定、菱形的判定、勾股定理等知识;本题综合性强,有一定难度,熟练掌握折叠的性质是解决问题的关键.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
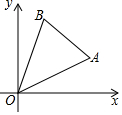 如图,在平面直角坐标系中,点A(a,b),B(c,a)均在第一象限,且c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$(b<a<3b)
如图,在平面直角坐标系中,点A(a,b),B(c,a)均在第一象限,且c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$(b<a<3b)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
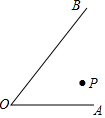 如图所示,在∠AOB内有一点P.
如图所示,在∠AOB内有一点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
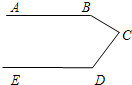 如图,一环湖公路的AB段为东西方向,经过三次拐弯后,又变成了东西方向的ED段,则∠B+∠C+∠D的度数为( )
如图,一环湖公路的AB段为东西方向,经过三次拐弯后,又变成了东西方向的ED段,则∠B+∠C+∠D的度数为( )| A. | 180° | B. | 270° | C. | 360° | D. | 450° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学活动课上,老师组织学生测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面还多1米,当同学们把绳子的下端拉开5米后,发现绳子下端刚好接触地面,请你根据题意画出图形,并求旗杆的高度.
数学活动课上,老师组织学生测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面还多1米,当同学们把绳子的下端拉开5米后,发现绳子下端刚好接触地面,请你根据题意画出图形,并求旗杆的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com