
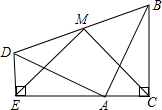
 两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由.
两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由. 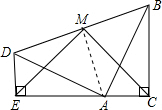 解:△EMC是等腰直角三角形.理由如下:
解:△EMC是等腰直角三角形.理由如下:| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3n+2 |
| 12 |
| 3n+2 |
| 12 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
用两个全等的含30°角的直角三角形制作如图1所示的两种卡片,两种卡片中扇形的 半径均为1, 且扇形所在圆的圆心分别为长直角边的中点和30°角的顶点, 按先A后B 的顺序交替摆放A、B两种卡片得到图2所示的图案. 若摆放这个图案共用两种卡片8张,则这个图案中阴影部分的面积之和为 ; 若摆放这个图案共用两种卡片(2n+1)张( n为正整数), 则这个图案中阴影部分的面积之和为 . (结果保留p )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com