
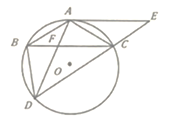
【题目】如图,在平行四边形ABCD中,连接AC,做△ABC的外接圆⊙O,延长EC交⊙O于点D,连接BD、AD,BC与AD交于点F分,∠ABC=∠ADB。
(1)求证:AE是⊙O的切线;
(2)若AE=12,CD=10,求⊙O的半径。
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)作辅助线,先根据垂径定理得:OA⊥BC,再证明OA⊥AE,则AE是⊙O的切线;
(2)连接OC,证明△ACE∽△DAE,得![]() ,计算CE的长,设⊙O的半径为r,根据勾股定理得:r2=62+(r-2
,计算CE的长,设⊙O的半径为r,根据勾股定理得:r2=62+(r-2![]() )2,解出可得结论.
)2,解出可得结论.
(1)证明:连接OA,交BC于G,
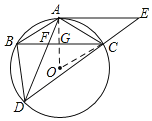
∵∠ABC=∠ADB.∠ABC=∠ADE,
∴∠ADB=∠ADE,
∴![]() ,
,
∴OA⊥BC,
∵四边形ABCE是平行四边形,
∴AE∥BC,
∴OA⊥AE,
∴AE是⊙O的切线;
(2)连接OC,
∵AB=AC=CE,
∴∠CAE=∠E,
∵四边形ABCE是平行四边形,
∴BC∥AE,∠ABC=∠E,
∴∠ADC=∠ABC=∠E,
∴△ACE∽△DAE,![]() ,
,
∵AE=12,CD=10,
∴AE2=DECE,
144=(10+CE)CE,
解得:CE=8或-18(舍),
∴AC=CE=8,
∴Rt△AGC中,AG=![]() =2
=2![]() ,
,
设⊙O的半径为r,
由勾股定理得:r2=62+(r-2![]() )2,
)2,
r=![]() ,
,
则⊙O的半径是![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
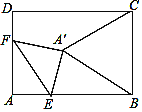
【题目】如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2![]() ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
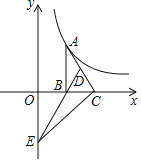
【题目】如图,已知点A在反比例函数y=![]() (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,过二次函数
为坐标原点,过二次函数![]() 图象上的点
图象上的点![]() ,作
,作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() .
.
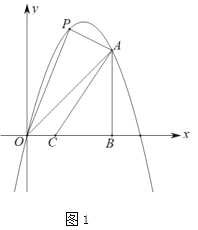
(1)如图1,![]() 为线段
为线段![]() 上方抛物线上的一点,在
上方抛物线上的一点,在![]() 轴上取点
轴上取点![]() ,点
,点![]() 、
、![]() 为
为![]() 轴上的两个动点,点
轴上的两个动点,点![]() 在点
在点![]() 的上方且
的上方且![]() 连接
连接![]() ,当四边形
,当四边形![]() 的面积最大时,求
的面积最大时,求![]() 的最小值.
的最小值.
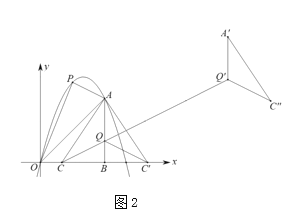
(2)如图2,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,
翻折,![]() 点的对应点为
点的对应点为![]() ,将
,将![]() 沿射线
沿射线![]() 平移
平移![]() 个单位得
个单位得![]() ,在抛物线上取一点
,在抛物线上取一点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知,在![]() 中,
中,![]() ,求作
,求作![]() 的内心
的内心![]() ,以下甲乙两同学的做法:
,以下甲乙两同学的做法:
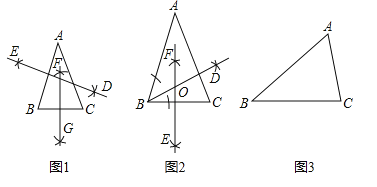
甲:如图1
①作![]() 垂直平分线
垂直平分线![]()
②作![]() 的垂直平分线
的垂直平分线![]()
③![]() 交于点
交于点![]()
则点![]() 即为所求
即为所求
乙:如图2
①作![]() 的角平分线
的角平分线![]()
②作![]() 的垂直平分线EF
的垂直平分线EF
③![]() 交于点
交于点![]()
则点![]() 即为所求
即为所求
甲同学的做法__________;乙同学的做法__________(填写正确或不正确)
(2)如图3![]() 中,
中, ![]() ,
,
①用直尺和圆规在![]() 的内部作射线
的内部作射线![]() ,使
,使![]() (不写作法,保留痕迹)
(不写作法,保留痕迹)
②若①中的射线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
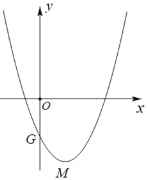
【题目】已知抛物线![]() :
:![]() (m>0)的顶点为M,交y轴于点G.
(m>0)的顶点为M,交y轴于点G.
(1)如图,若点G坐标为(0,![]() )
)
①直接写出抛物线![]() 解析式;
解析式;
②点Q在y轴上,将线段QM绕点Q逆时针旋转90°得线段QN,若点N恰好落在抛物线![]() 上,求点Q的坐标.
上,求点Q的坐标.
(2) 探究: 将抛物线![]() 沿唯一的定直线x=a对称得抛物线
沿唯一的定直线x=a对称得抛物线![]() ,记抛物线
,记抛物线![]() 交y轴于点P (0,-2m),求a的值.
交y轴于点P (0,-2m),求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能状况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行统计,绘制成图(1)和图(2)两幅尚不完整的统计图.
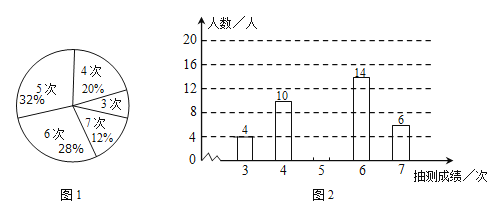
(1)本次抽取的男生有 人,抽取成绩的众数是 ;
(2)请你在图(2)补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,该校九年级男生共有900人,则估计有多少人体能达标?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com