
【题目】△ABC,AB=AC,AC的垂直平分线与AB所在直线相交所得的锐角为40°,∠C=______.
【答案】65°或25°
【解析】
当△ABC为锐角三角形时,设AC的垂直平分线交线段AB于点D,交AC于点E,在Rt△ADE中可求得∠A,再由三角形内角和定理可求得∠C;当△ABC为钝角三角形时,设AC的垂直平分线交AC于点E,交直线AB于点D,则可求得△CAB的外角,再利用外角的性质可求得∠C,可求得答案.
解:当△ACB为锐角三角形时,如图1,设AC的垂直平分线交线段AB于点D,交AC于点E,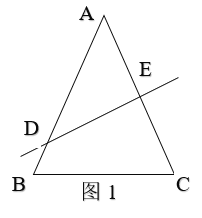
∵∠ADE=40°,DE⊥AC,
∴∠A=90°-40°=50°,
∵AC=AB,
∴∠C=![]() (180°-∠A)=65°;
(180°-∠A)=65°;
当△ABC为钝角三角形时,如图2,设AC的垂直平分线交AC于点E,交AB于点D,
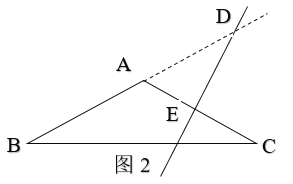
∵∠ADE=40°,DE⊥AC,
∴∠DAC=50°,
∵AC=AB,
∴∠C=∠B,
∵∠C+∠B=∠DAC,
∴∠C=25°;
故答案为: 65°或25°,


科目:初中数学 来源: 题型:
【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 220 | 180 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠A=∠B=70°.请按如下要求操作并解答:

(1)在图中,过点A画直线MP∥BC,过点C画直线NP⊥AB,直线MP与NP交于点P,求∠APC的度数;
(2)在(1)的前提下,直线PM上存在点D,且∠ABD=∠ADB,求直线BD与直线PN相交所形成的锐角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量![]() (毫克)随时间
(毫克)随时间![]() (小时)的变化情况如图所示,当成年人按规定剂量服药后.
(小时)的变化情况如图所示,当成年人按规定剂量服药后.

(1)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是________;
之间的函数关系式是________;
(2)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是______;
之间的函数关系式是______;
(3)如果每毫升血液中含药量![]() 毫克或
毫克或![]() 毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
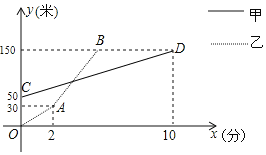
【题目】一直线上有A、B、C不同三地,甲、乙两人分别从A、B两地同时同向出发前往距离B地150米的C地,甲、乙两人距离B地的距离y(米)与行走试卷x(分)之间的关系图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速行走,且乙在加速后的速度是甲速度的4倍.
(1)乙加速之后的速度为 米/分;
(2)求当乙追上甲时两人与B地的距离;
(3)当甲出发 分钟时,两人相距10米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,发现代数式2m2+5mn+2n2可以因式分解为 ;
(3)若每块小矩形的面积为10cm2,四个正方形的面积和为58cm2,试求(m+n)2的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com