
已知:关于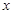 的一元二次方程
的一元二次方程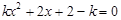 .
.
(1)求实数k的取值范围;
(2)设上述方程的两个实数根分别为x1、x2,求:当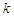 取哪些整数时,x1、x2均为整数;
取哪些整数时,x1、x2均为整数;
(3)设上述方程的两个实数根分别为x1、x2,若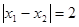 ,求k的值.
,求k的值.
(1)k≠0;(2)k=±1或者k=±2;(3) 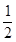 .
.
【解析】
试题分析:(1)一元二次方程存在的条件是二次项系数不为零,根据题意,kx2+2x+2-k=0是关于x的一元二次方程,所以k≠0;(2)根据求根公式,可以将方程的解求出来,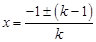 ,
, ,
, ,要使得方程的根为整数,只要要求
,要使得方程的根为整数,只要要求 是整数即可,进而只要要求
是整数即可,进而只要要求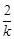 为整数,k是2的因数,所以k=±1或者k=±2;(3)方法一:由(2)可以得到
为整数,k是2的因数,所以k=±1或者k=±2;(3)方法一:由(2)可以得到  ,
, ,所以
,所以 ,分类讨论,①当
,分类讨论,①当 时,此方程无解;②当
时,此方程无解;②当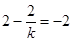 时,解得
时,解得 ;方法二:可以根据根与系数关系
;方法二:可以根据根与系数关系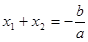 ,
, 进行求解,具体详见解析.
进行求解,具体详见解析.
试题解析:(1) ∵方程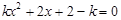 是关于x的一元二次方程,
是关于x的一元二次方程,
∴实数k的取值范围是k≠0.
(2)△= b2-4ac=4-4k(2-k)=k2-2k+1=(k-1)2 ,
由求根公式,得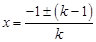 ,
,
∴ ,
, ,
,
∵要求两个实数根x1、x2是整数,
∴ 为整数,即
为整数,即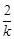 是整数,
是整数,
∴k是2的因数, k=±1或者k=±2.
(3)方法一:由(2)可以得到  ,
, ,
,
∴ ,分类讨论:
,分类讨论:
①当 时,此方程无解;
时,此方程无解;
②当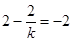 时,解得
时,解得 ;
;
方法二:根据题意,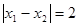 ,两边平方,有
,两边平方,有 ,
,
整理得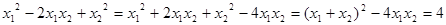 ,
,
由根与系数的关系 ,
, ,
,
∴ ,
,
整理,得8k-4=0,k=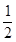 .
.
考点:1.一元二次方程的求解和根与系数关系;2.绝对值的化简.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
(12分)如图,已知关于![]() 的一元二次函数
的一元二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.

1.⑴ 求出一元二次函数的关系式;
2.⑵点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
3.⑶ 探索线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为直角三角形,如果存在,求出
为直角三角形,如果存在,求出![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 (12分)如图,已知关于
(12分)如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
 点
点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围; 上是否存在点
上是否存在点 ,使得
,使得 为直角三角形,如果存在,求出
为直角三角形,如果存在,求出 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2013届江苏省仪征市九年级第二次模拟考试数学试卷(带解析) 题型:解答题
如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与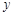 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
(1)求出一元二次函数的关系式;
(2)点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)在(2)的条件下,当 点坐标是 时,
点坐标是 时,  为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省泰州市永安初级中学九年级下学期第二次涂卡训练数学试卷(带解析) 题型:解答题
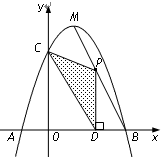
如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
(1)求出一元二次函数的关系式;
(2)点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为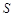 ,求
,求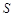 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)在(2)的条件下,当 点坐标是 时,
点坐标是 时, 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省泰州市九年级下学期第二次涂卡训练数学试卷(解析版) 题型:解答题
如图,已知关于 的一元二次函数
的一元二次函数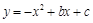 (
( )的图象与
)的图象与 轴相交于
轴相交于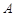 、
、 两点(点
两点(点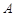 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.

(1)求出一元二次函数的关系式;
(2)点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)在(2)的条件下,当 点坐标是 时,
点坐标是 时, 为直角三角形.
为直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com