
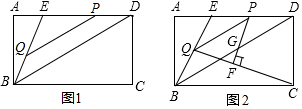
���� ��1���ȹ�����E��EM��QP����ΪM����Rt��EQP�У��á�EBD=��EDB=30�㣻�����ɵ�PE=$\frac{\sqrt{3}}{3}$PQ����BE=DE�����ɵó�BE=PD+$\frac{\sqrt{3}}{3}$PQ���������ʽ�ɵ�y��x�Ĺ�ϵ��
��2������PC��BD�ڵ�N���ɵá�QPC=90�㣬�����ɵá�PNG�ס�QPC���ɵ�$\frac{PG}{QC}=\frac{PN}{PQ}$����ɵ�PG�ij���
��� �⣺�ߡ�A=90���ABE=30�㣬
���AEB=60�㣮
��EB=ED��
���EBD=��EDB=30�㣮
��PQ��BD��
���EQP=��EBD��
��EPQ=��EDB��
���EPQ=��EQP=30�㣬
��EQ=EP��
����E��EM��QP����ΪM����PQ=2PM��
�ߡ�EPM=30�㣬
��PM=$\frac{\sqrt{3}}{2}$PE��PE=$\frac{\sqrt{3}}{3}$PQ��
��BE=DE=PD+PE��
��BE=PD+$\frac{\sqrt{3}}{3}$PQ��
������֪AE=$\frac{1}{2}$BE��
��DE=BE=2AE��
��AD=BC=6��
��2AE=DE=BE=4��
�ߵ���P���߶�ED�ϣ�
����Q��QH��AD�ڵ�H����QH=$\frac{1}{2}$PQ=$\frac{1}{2}$x��
�ɣ�1����PD=BE-$\frac{\sqrt{3}}{3}$x��PD=4-$\frac{\sqrt{3}}{3}$x��
��y=$\frac{1}{2}$PD•QH=-$\frac{\sqrt{3}}{12}$x2+x��
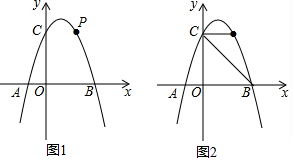
��3���⣺����PC��BD�ڵ�N����ͼ3����
�ߵ�P���߶�ED�е㣬
��EP=PD=2��PQ=2$\sqrt{3}$��
��DC=AB=AE•tan60��=2$\sqrt{3}$��
��PC=$\sqrt{P{D}^{2}+D{C}^{2}}$=4��
��cos��DPC=$\frac{PD}{PC}$=$\frac{1}{2}$��
���DPC=60�㣮
���QPC=180��-��EPQ-��DPC=90�㣮
��PQ��BD��
���PND=��QPC=90�㣮
��PN=$\frac{1}{2}$PD=1��
QC=$\sqrt{P{Q}^{2}+P{C}^{2}}$=2$\sqrt{7}$��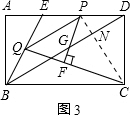
�ߡ�PGN=90��-��FPC����PCF=90��-��FPC��
���PGN=��PCF��
�ߡ�PNG=��QPC=90�㣬
���PNG�ס�QPC��
��$\frac{PG}{QC}=\frac{PN}{PQ}$��
��PG=$\frac{1}{2\sqrt{3}}$��$2\sqrt{7}$=$\frac{\sqrt{21}}{3}$��
���� �������ı����ۺ��⣬��Ҫ�����˾��ε����ʣ������ε������ʽ�����ɶ�����������Ǻ��������������ε����ʺ��ж����Ȿ��Ĺؼ��ǵó�BE=PD+$\frac{\sqrt{3}}{3}$PQ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4��10-5 | B�� | 0.4��10-6 | C�� | 4��10-4 | D�� | 40��10-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
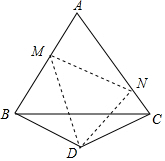 ��ͼ����ABC�DZ߳�Ϊ10cm�ĵȱ������Σ���BDC�ǵ��������Σ��ҡ�BDC=120�㣮��DΪ������һ��60��ǣ�ʹ�����߷ֱ�AB�ڵ�M����AC�ڵ�N������MN�����AMN���ܳ�Ϊ20��
��ͼ����ABC�DZ߳�Ϊ10cm�ĵȱ������Σ���BDC�ǵ��������Σ��ҡ�BDC=120�㣮��DΪ������һ��60��ǣ�ʹ�����߷ֱ�AB�ڵ�M����AC�ڵ�N������MN�����AMN���ܳ�Ϊ20���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
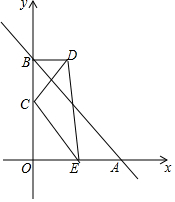 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��0��4������E��2��0����OA�ϣ���C������Ϊ��0��m����m��4������C����AB�ĶԳƵ��ǵ�D������BD��CD��CE��DE
��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��0��4������E��2��0����OA�ϣ���C������Ϊ��0��m����m��4������C����AB�ĶԳƵ��ǵ�D������BD��CD��CE��DE�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
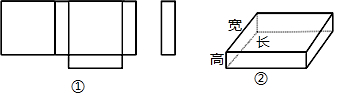
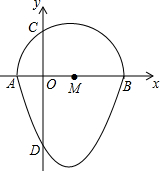 ���ǰ�һ����Բ�������ߵ�һ������ɵķ��ͼ�γ�Ϊ����Բ������ͼ��A��B��C��D�ֱ���ij��Բ��������Ľ������������ߵĽ���ʽΪy=x2-2x-3����Բ������CD�ij�Ϊ3+$\sqrt{3}$��
���ǰ�һ����Բ�������ߵ�һ������ɵķ��ͼ�γ�Ϊ����Բ������ͼ��A��B��C��D�ֱ���ij��Բ��������Ľ������������ߵĽ���ʽΪy=x2-2x-3����Բ������CD�ij�Ϊ3+$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com