
【题目】正方形ABCD中,点P为直线BC上的一点,DP的垂直平分线交射线DC于M,交DP于E,交射线AB于N.
(1)当点M在CD边上时如图①,易证PM-CP=AN;
(2)当点M在CD边延长线上如图②、图③的位置时,上述结论是否成立?写出你的猜想,并对图②给予证明.



图① 图② 图③
【答案】图②:PM+CP=AN;图③:PM-CP=AN,证明见解析.
【解析】(1)过N作NQ∥AD,则NQ=AD,AN=DQ,易证∠MNQ=∠PDC,即可证明△MNQ≌△PDC,可得QM=PC,再根据垂直平分线性质可得DM=PM,即可解题;
(2)①作MQ∥BF,则AQ=DM,QM=AD=CD,易证∠NMQ=∠MDE,即可证明△NMQ≌△PDC,可得QN=PC,再根据垂直平分线性质可得PM=AQ,即可解题;
③作NQ∥BC,则NQ=AD=CD,AN=DQ,易证∠NMD=∠CPD,即可证明△CDP≌△EDM,可得QM=CP,再根据垂直平分线性质可得DM=PM,即可解题.
证明:(1)过N作NQ∥AD,则NQ=AD,AN=DQ,
∵MN是PD垂直平分线,
∴DM=PM,
∵∠NMQ+∠MNQ=90°,∠NMQ+∠PDC=90°,
∴∠MNQ=∠PDC,
∵在△MNQ和△PDC中,
∠MQN=∠PCD=90°,NQ=CD,∠MNQ=∠PDC
∴△MNQ≌△PDC,(ASA)
∴QM=PC,
∵DM=DQ+QM,
∴PM=AN+PC,即PM-CP=AN;
(2)①M在图②位置时,不成立,新结论为AN=PM+CP;
理由:作MQ∥BF,则AQ=DM,QM=AD=CD,∠QMD=90°,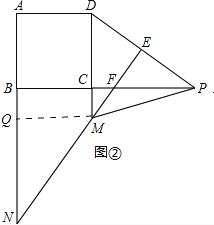
∵EF是PD垂直平分线,∴DM=PM,
∴PM=AQ,
∵∠NMQ+∠DME=90°,∠DME+∠MDE=90°,
∴∠NMQ=∠MDE,
∵在△NMQ和△PDC中,
∠NMQ=∠MDE,QM=CD,∠MQN=∠DCP=90°
∴△NMQ≌△PDC,(ASA)
∴QN=PC,
∵AN=AQ+QN,
∴AN=PM+CP;
②M在图③位置时,成立,
理由:作NQ∥BC,则NQ=AD=CD,AN=DQ,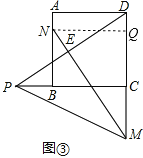
∵EM是PD的垂直平分线,
∴DM=PM,
∵∠NMD+∠MDE=90°,∠CPD+∠MDE=90°,
∴∠NMD=∠CPD,
∵在△CDP和△EDM中,
∠NMD=∠CPD,∠MQN=∠PCD,CD=NQ
∴△CDP≌△EDM,(AAS)
∴QM=CP,
∵DM=QM+DQ,
∴PM=AN+CP,即PM-CP=AN.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】 将抛物线y=x2-2x+1向下平移2个单位,再向左平移1个单位,所得抛物线的解析式是( )
A.y=x2-2x-1B.y=x2+2x-1C.y=x2-2D.y=x2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学家研究发现,声音在空气中传播的速度y(米/秒)与气温x(°C)有关,当气温是0°C时,音速是331米/秒;当气温是5°C时,音速是334米/秒;当气温是10°C时,音速是337米/秒;气温是15°C时,音速是340米/秒;气温是20℃时,音速是343米/秒;气温是25°C时,音速是346米/秒;气温是30°C时,音速是349米/秒.
(1)请你用表格表示气温与音速之间的关系;
(2)表格反映了哪两个变量之间的关系?哪个是自变量?哪一个是对应的值?
(3)当气温是35°C时,估计音速y可能是多少?
(4)能否用一个式子来表示两个变量之间的关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(3,4),B(5,0),C(0,﹣2).在第一象限找一点D,使四边形AOBD成为平行四边形,
(1)点D的坐标是;
(2)连接OD,线段OD、AB的关系是;
(3)若点P在线段OD上,且使PC+PB最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.

(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com