
【题目】 “十![]() 一”黄金周期间,西安大唐芙蓉园在7天假期中每天接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)。
一”黄金周期间,西安大唐芙蓉园在7天假期中每天接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)。
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 (万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.4 |
(1)若9月30日的游客人数为![]() 万人,则10月2日的游客人数为_______万人;
万人,则10月2日的游客人数为_______万人;
(2)七天内游客人数最大的是10月_______日;
(3)若9月30日游客人数为3万人,门票每人120元。请求出黄金周期间西安大唐芙蓉园门票总收入是多少万元?
【答案】(1)a+2.4;(2)3;(3)总收入为2568万元.
【解析】
试题分析:(1)10月2日的游客人数=a+1.6+0.8.
(2)分别用a的代数式表示七天内游客人数,再找出最多的人数,以及对应的日期即可.
(3)求出总人数,再乘以门票的单价,就看看得到总收入.
试题解析:(1)a+1.6+1.8=a+2.4(万人),
(2)3七天内游客人数分别是a+1.6,a+2.4,a+2.8,a+2.4,a+1.6,a+1.8,a+0.6,
所以3日人最多.
(3)依题意得黄金周游客总人数为:
21+(1.6+0.8+0.4-0.4-0.8+0.2-1.4)=21.4(万人)
那么,总收入为21.4×120=2568万元
答:总收入为2568万元.


科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复以上步骤,下表为实验的一组统计数据:
摸球的次数n | 1000 | 1500 | 2000 | 5000 | 8000 | 10000 |
摸到白球的次数m | 582 | 960 | 1161 | 2954 | 4842 | 6010 |
摸到白球的频率 | 0.582 | 0.64 | 0.5805 | 0.5908 | 0.6053 | 0.601 |
请估算口袋中白球的个数约为( )
A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
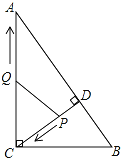
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)当t为何值时,△CPQ为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第![]() (1≤
(1≤![]() ≤90)天的售价与销量的相关信息如下表:
≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BD是AC边上的中线,延长BC到E,使CE=CD.
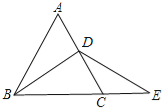
问:
(1)DB与DE相等吗?
(2)把BD是AC边上的中线改成什么条件,还能得到同样的结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1厘米/秒的速度向点A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为35平方厘米?PQ的距离是多少厘米?(结果用最简二次根式表示)
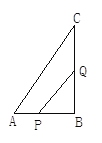
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:
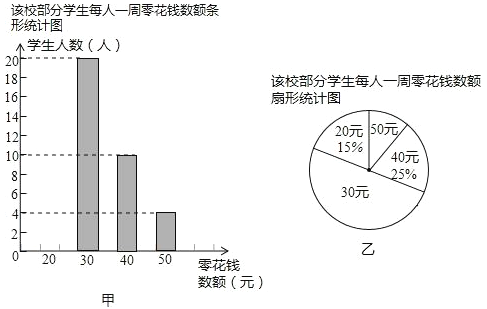
(1)校团委随机调查了多少学生?请你补全条形统计图;
(2)表示“50元”的扇形的圆心角是多少度?被调查的学生每人一周零花钱数的中位数是多少元?
(3)四川雅安地震后,全校1000名学生每人自发地捐出一周零花钱的一半,以支援灾区建设.请估算全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com