
分析 首先化简x的值,把分式的分子和分母分解因式,进行化简,然后把x的值代入求解.
解答 解:x=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$<1.
原式=$\frac{(x+1)(x-1)}{x-1}$-$\frac{\sqrt{(x-1)^{2}}}{x(x-1)}$
=x+1-$\frac{1-x}{x(x-1)}$
=x+1+$\frac{1}{x}$,
当x=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$是,原式=2-$\sqrt{3}$+1-(2+$\sqrt{3}$)=2-$\sqrt{3}$+1-2-$\sqrt{3}$=1-2$\sqrt{3}$.
点评 本题考查了分式和根式的化简求值,正确根据根式的形式,化简根式是关键.


科目:初中数学 来源: 题型:解答题
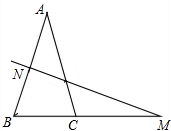 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
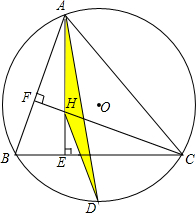 已知,△ABC内接于⊙O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.
已知,△ABC内接于⊙O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com