
【题目】李大爷一年前买入了A、B两种兔子共46只.目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只.
(1)则一年前李大爷买入A种兔子________只,目前A、B两种兔子共________只(用含a的代数式表示);
(2)若一年前买入的A种兔子数量多于B种兔子数量,则目前A、B两种兔子共有多少只?
(3)李大爷目前准备卖出30只兔子,已知卖A种兔子可获利15元/只,卖B种兔子可获利6元/只.如果卖出的A种兔子少于15只,且总共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?请求出最大获利.
【答案】(1)![]() ,43-a;(2) 当a=1时,A、B两种兔子有42只;(3) 方案一:卖出的A种兔子12只,B种兔子18只,可获利12×15+18×6=288(元),方案二:卖出的A种兔子13只,B种兔子17只,可获利13×15+17×6=297(元),方案三:卖出的A种兔子14只,B种兔子16只,可获利14×15+16×6=306(元),方案三获利最大,最大利润为306元
,43-a;(2) 当a=1时,A、B两种兔子有42只;(3) 方案一:卖出的A种兔子12只,B种兔子18只,可获利12×15+18×6=288(元),方案二:卖出的A种兔子13只,B种兔子17只,可获利13×15+17×6=297(元),方案三:卖出的A种兔子14只,B种兔子16只,可获利14×15+16×6=306(元),方案三获利最大,最大利润为306元
【解析】
(1)利用目前他所养的这两种兔子数量相同,得出等式求解即可;(2)利用一年前买入的兔子数量多于B种兔子数量,得出不等式求解即可;(3)利用总共获利不低于280元,卖A种兔子可获利15元/只,卖B种兔子可获利6元/只,得出不等关系,进而利用A种兔子的数量取值范围得出即可.
(1)![]() ;43﹣a
;43﹣a
(2)解:由题意得出:![]() >
>![]() , 解得:a<3,
, 解得:a<3,
由题意得:a,![]() ,
,![]() 应为正整数,
应为正整数,
当a=1时,符合题意,即目前A、B两种兔子有42只;
当a=2时,![]() ,
,![]() 为分数,不合题意;
为分数,不合题意;
∴当a=1时,A、B两种兔子有42只
(3)解:设李大爷卖出A种兔子y只,则卖出B种兔子(30﹣y)只,由题意得出: 15y+(30﹣y)×6≥280,
解得:y≥![]() ,
,
又∵卖出的A种兔子少于15只,即 ![]() ≤y<15,
≤y<15,
∵y是整数,
∴y=12,13,14,即李大爷有三种卖兔方案:
方案一:卖出的A种兔子12只,B种兔子18只,可获利12×15+18×6=288(元),
方案二:卖出的A种兔子13只,B种兔子17只,可获利13×15+17×6=297(元),
方案三:卖出的A种兔子14只,B种兔子16只,可获利14×15+16×6=306(元),
显然,方案三获利最大,最大利润为306元.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+x﹣2与x轴交于A,B两点,与y轴交于点C.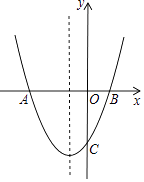
(1)求点A,点B和点C的坐标;
(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;
(3)若点M是直线AC下方抛物线上一动点,求四边形ABCM面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π). 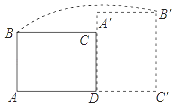
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣8mx+16m﹣1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2﹣8mx+16m﹣1(m>0)与线段CD有交点,请写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+(m﹣1)x+m与y轴交点坐标是(0,3).
(1)求出m的值并画出这条抛物线; 
(2)求抛物线与x轴的交点和抛物线顶点的坐标;
(3)当x取什么值时,y的值随x值的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
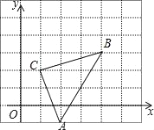
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2)
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ ( 、 )
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(2,3),B(1,1),C(4,1),M(6,3).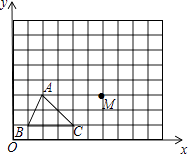
(1)将△ABC平原得到△A1B1C1 , 其中点A,B,C的对应点分别是A1 , B1 , C1 , 且点A1的坐标是(3,6),在图中画出△A1B1C1 .
(2)将(1)中的△A1B1C1绕点M顺时针旋转90°,画出旋转后的△A2B2C2(其中点A2 , B2 , C2的对应点分别是A1 , B1 , C1),并写出点A2 , B2 , C2的坐标.
(3)(2)中的△A2B2C2能通过旋转△ABC得到吗?若能,请写出旋转的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com