【题目】如图，在等腰三角形
中，
，
为
边上中点，过点作
，交
于
，交
于
，若
，则的长为_________．
【答案】6
【解析】
连接BD，利用ASA证出△EDB≌△FDC，从而证出S△EDB=S△FDC，从而求出S△DBC，然后根据三角形的面积即可求出CD，从而求出AC，最后利用勾股定理即可求出结论．
解：连接BD
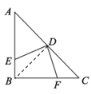
∵在等腰三角形
中，
，
为
边上中点，
∴AB=BC，BD=CD=AD，∠BDC=90°，∠EBD=
，∠C=45°
∵
∴∠EDF=∠BDC=90°，∠EBD=∠C=45°
∴∠EDB=∠FDC
在△EDB和△FDC中
∴△EDB≌△FDC
∴S△EDB=S△FDC
∴S△DBC= S△FDC＋S△BDF= S△EDB＋S△BDF=
∴
∴CD2=18
∴CD=
∴AC=2CD=
∴AB2＋BC2=AC2
∴2AB2=（）2
故答案为：6．
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目：初中数学 来源： 题型：
【题目】甲、乙两人分别骑自行车和摩托车，从同一地点沿相同的路线前往距离80km的某地，图中l1，l2分别表示甲、乙两人离开出发地的距离s（km）与行驶时间t（h）之间的函数关系．请根据图象解答下列问题：
（1）甲、乙两人谁到达目的地较早？早多长时间？
（2）分别求甲、乙两人行驶过程中s与t的函数关系式；
（3）试确定当两辆车都在行驶途中（不包括出发地和目的地）时，t的取值范围；并在这一时间段内，求t为何值时，摩托车行驶在自行车前面？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．
（1）在图1中证明CE=CF；
（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；
（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形ABCD的对角线相交于点O，AC＝2，BD＝2
，将菱形按如图方式折叠，使点B与点O重合，折痕为EF，则五边形AEFCD的周长为_____________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD中，∠D＝100°，AC平分∠BCD，且∠ACB＝40°，∠BAC＝70°.
(1)AD与BC平行吗？试写出推理过程；
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°．
（1）求证：△ABD∽△DCE；
（2）若BD=3，CE=2，求△ABC的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列关于函数
的四个命题：①当
时， 
有最小值10；②
为任意实数， 
时的函数值大于
时的函数值；③若
，且
是整数，当
时， 
的整数值有
个；④若函数图象过点
和
，其中
， 
，则
．其中真命题的序号是（ ）
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某班级为准备元旦联欢会，欲购买价格分别为2元、4元和10元的三种奖品，每种奖品至少购买一件，共买16件，恰好用50元.若2元的奖品购买a件.
(1)用含a的代数式表示另外两种奖品的件数；
(2)请你设计购买方案，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】端午节三天假期的某一天，小明全家上午8时自驾小汽车从家里出发，到章丘某旅游景点游玩．该小汽车离家的距离S（千米）与时间t（小时）的关系如图所示．根据图象提供的有关信息，下列说法中错误的是（ ）
A. 景点离小明家180千米 B. 小明到家的时间为17点
C. 返程的速度为60千米每小时 D. 10点至14点，汽车匀速行驶
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com