解:(1)依题意得△=0,即
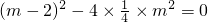
,
-4m+4=0,
解得m=1,
当m=1时,原方程为
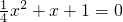
解得x
1=x
2=-2.
(2)不存在.
假设存在正数m使得x
12+x
22=224,
则由韦达定理得x
1+x
2=4m-8,x
1x
2=4m
2,
∴x
12+x
22=(x
1+x
2)
2-2x
1x
2=(4m-8)
2-8m
2=224,
即:m
2-8m-20=0,
解得m
1=10,m
2=-2(舍去)
∵
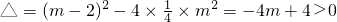
,
∴m<1
∴m
1=10也不符合题意,应舍去.
故不存在正数m使得方程两根满足x
12+x
22=224.
分析:(1)由△=0,即
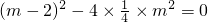
得到m的方程,可求得m的值,再把m的值代入原方程,解方程即可;
(2)先假设存在正数m使得x
12+x
22=224,然后利用根与系数的关系x
1+x
2=4m-8,x
1x
2=4m
2.于是有x
12+x
22=(x
1+x
2)
2-2x
1x
2=(4m-8)
2-8m
2=224,解方程求出m的值,同时由△>0得m<1,且m为正数,最后确定不存在符合条件的正数m
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.考查了根与系数的关系x
1+x
2=-

,x
1x
2=

.也考查了存在性问题的解题方法和格式.

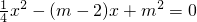 .
.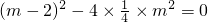 ,
,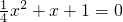
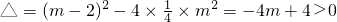 ,
,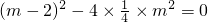 得到m的方程,可求得m的值,再把m的值代入原方程,解方程即可;
得到m的方程,可求得m的值,再把m的值代入原方程,解方程即可; ,x1x2=
,x1x2= .也考查了存在性问题的解题方法和格式.
.也考查了存在性问题的解题方法和格式. 

 导学教程高中新课标系列答案
导学教程高中新课标系列答案