
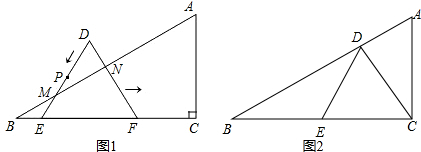
分析 (1)如图1中,作CH⊥AB于H,求出CH的长即可.
(2)本题要先找出几个关键点:当P与M重合时,那么根据P的速度可表示出DM的长,而ME=BE为三角形平移的距离,据此可求出t=1.当P到达E点时,DP=DE,可求得此时t=$\frac{3}{2}$.①当P在DM之间时,即0≤x<1,MN的长可在直角三角形DMN中,根据DM和∠DMN的余弦值求出,过P作PP1⊥MN于P1,那么PP1就是MN边上的高,可在RT△MPP1中根据MP的长和∠PMP1的正弦值求出(MP可根据DE-DP-ME来得出).据此可得出关于S,x函数关系式.②当P在EM之间时,即1<x≤$\frac{3}{2}$,可过P作PP2⊥AB与P2,那么PP2的长可在直角三角形PP2M中,根据PM的长和∠BME的正弦值求出,进而可根据三角形的面积公式求出S、x的函数关系式.③当P在EF上运动时,即$\frac{3}{2}$≤x≤3,解法同上.
(3)①如图5中,当点G在线段CK上时,根据S△HKG=S△DHE+S四边形DECK-S△HEG-S△BCG=$\frac{\sqrt{3}}{2}$列出方程即可解决.②如图6中,当点G在线段AK上上,根据S△HGK=S△HEG+S△ECG-S△EDH-S四边形DECK=$\frac{\sqrt{3}}{2}$列出方程即可解决.
解答 解:(1)如图1中,作CH⊥AB于H,由题意等边三角形的边长为CH,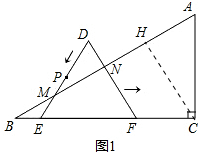
∵∠c=90°∠A=60°,
∴∠B=30°,∠ACH=30°,
∴∠ADC=90°,
∴AH=$\frac{1}{2}$AC,
∵BC=6,
∴AC=2$\sqrt{3}$,
∴AH=$\sqrt{3}$,
∴CH=$\sqrt{3}$AH=3.
∴△DEF的边长为3.
(2)如图2中,在Rt△DMN中,DM=3-x,MN=(3-x)×cos30°=$\frac{\sqrt{3}}{2}$(3-x),
当P点运动到M点时,有2x+x=3,
∴x=1
①如图2中,当P点在DM之间运动时,过P点作PP1⊥AB,垂足为P1,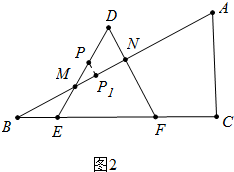
在Rt△PMP1中,∵∠PP1M=90°,PM=3-x-2x=3-3x,∠PMP1=30
∴PP1=$°\frac{1}{2}$PM=$\frac{1}{2}$(3-3x)=$\frac{3}{2}$(1-x),
∴y与x的函数关系式为:y=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$(3-x)×$\frac{3}{2}$(1-x)=$\frac{3\sqrt{3}}{8}$(x2-4x+3)(0≤x<1),(x=1时,三角形不存在)
②如图3中,当P点在ME之间运动时,过P点作PP2⊥AB,垂足为P2,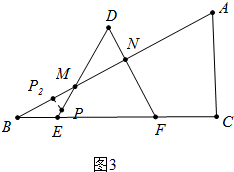
在Rt△PMP2中,∵∠PP2M=90°,PM=x-(3-2x)=3(x-1),∠PMP2=30°,
∴PP1=$\frac{3}{2}$(1-x),
∴y与x的函数关系式为:y=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$(3-x)×$\frac{3}{2}$(1-x),
=-$\frac{3\sqrt{3}}{8}$(x2-4x+3)(1<x≤$\frac{3}{2}$).
③如图4中,当P点在EF之间运动时,过P点作PP3⊥AB,垂足为P3,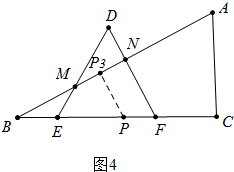
在Rt△PMP3中,PB=x+(2x-3)=3(x-1),
∴PP3=$\frac{3}{2}$(x-1),
∴y与x的函数关系式为:y=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$(3-x)×$\frac{3}{2}$(x-1),
=-3$\frac{3\sqrt{3}}{8}$(x2-4x+3)($\frac{3}{2}$≤x≤3),
(3)①如图5中,当点G在线段CK上时,∵∠KCD=∠KDC=30°,∠A=∠ADK=60°,
∴DK=AK=KC=$\sqrt{3}$,
∵S△HKG=S△DHE+S四边形DECK-S△HEG-S△BCG=$\frac{\sqrt{3}}{2}$,
∴3$\sqrt{3}$-$\frac{\sqrt{3}}{4}$(9+x2)=$\frac{\sqrt{3}}{2}$,
∴x2=1,
∵x>0,
∴x=1.
∴CG=1
②如图6中,当点G在线段AK上上,∵S△HGK=S△HEG+S△ECG-S△EDH-S四边形DECK=$\frac{\sqrt{3}}{2}$,
∴$\frac{\sqrt{3}}{4}$(9+x2)-3$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
∴x2=5,
∵x>0,
∴x=$\sqrt{5}$.
∴CG=$\sqrt{5}$.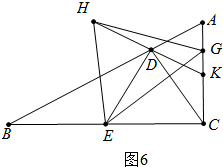
综上所述若△HGK的面积等于$\frac{\sqrt{3}}{2}$时,CG=1或$\sqrt{5}$.
点评 本题考查几何变换综合题、直角三角形30度角的性质、三角形面积公式、勾股定理等知识,解题的关键是学会分类讨论,正确画出图象,学会利用分割法求三角形面积,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果$\frac{AD}{BC}=\frac{1}{4}$,那么$\frac{AF}{BF}$的值是( )
如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果$\frac{AD}{BC}=\frac{1}{4}$,那么$\frac{AF}{BF}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
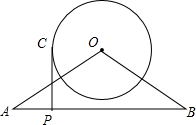 如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )| A. | 3≤PC≤3$\sqrt{17}$ | B. | 5≤PC≤13 | C. | 4≤PC≤3$\sqrt{17}$ | D. | 1<PC≤13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
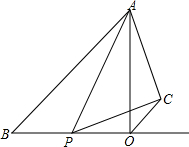 在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.
在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com