

分析 (1)分两种情形,①当点P在AE上时,由△APN∽△ACB可以解决问题,②当点P在ED上时,PN=3,求出AE+EP即可;
(2)当0<t≤3时,重叠部分图形为三角形,当3≤t≤6时,重叠部分图形为直角梯形,当6<t≤9,重叠部分是五边形,当9<t≤12,重叠部分是梯形,分四种情况分别求出S与t之间的函数关系式即可;
(3)分三种情形讨论:①当∠P1GH=90°,②当∠P1HG=90°,③当∠GP1H=90°,分别进行分析判断.
解答 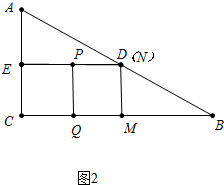
 解:(1)①如图1,当点P在AE上时,
解:(1)①如图1,当点P在AE上时,
∵PN∥BC,
∴△APN∽△ACB,
∴$\frac{AP}{AC}=\frac{PN}{BC}$,即$\frac{t}{6}$=$\frac{6-t}{12}$,
∴t=2;
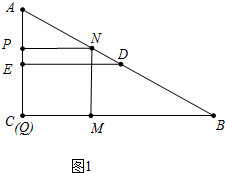
②如图2,当点P在ED上时,PN=3,
∴AE+EP=3+(6-3)=6,
∴t=6÷1=6;
综上,当t的值为2或6秒时,正方形PQMN的顶点N落在AB边上;
(2)如图,当0<t≤3时,重叠部分图形为三角形EGF,
由AP=t可得,PC=PN=EG=6-t,
由△EGF∽△BCE可得,$\frac{GF}{EG}=\frac{EC}{BC}$
即$\frac{GF}{6-t}=\frac{3}{12}$,
∴GF=$\frac{3}{2}-\frac{t}{4}$,
∴S=$\frac{1}{2}$×(6-t)×($\frac{3}{2}-\frac{t}{4}$)=$\frac{1}{8}{t}^{2}-\frac{3}{2}t+\frac{9}{2}$(0<t≤3);
如图,当3≤t≤6时,重叠部分图形为直角梯形PNFH,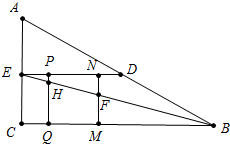
由AE+EP=t可得,EP=t-3,
由△EPH∽△BCE∽△ENF可得,PH=$\frac{t-3}{4}$,NF=$\frac{t}{4}$,
∴S=$\frac{1}{2}$×3×($\frac{t-3}{4}$+$\frac{t}{4}$)=$\frac{3}{4}t-\frac{9}{8}$(3≤t≤6);
如图,当6<t≤9,重叠部分是五边形PDKFH,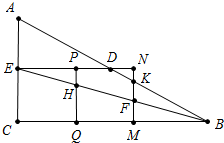
由AE+EP=t可得,EP=t-3,
由△EPH∽△BCE∽△ENF可得,PH=$\frac{t-3}{4}$,NF=$\frac{t}{4}$,
DN=t-3+3-6=t-6,由△DNK∽△DEA可得,NK=$\frac{t-6}{2}$,
∴S=S梯形PNFH-S△DNK=($\frac{3}{4}t-\frac{9}{8}$)-$\frac{1}{2}$×(t-6)×$\frac{t-6}{2}$=-$\frac{1}{4}{t}^{2}$+$\frac{15}{4}t$-$\frac{81}{8}$(6<t≤9);
如图,当9<t≤12,重叠部分是梯形PKFH,
由DP=$\sqrt{5}$(t-9),△DRP∽△DEA可得,DR=2(t-9),RP=t-9,
由△ERH∽△BCE可得,RH=$\frac{t}{2}-3$,
∴PH=6-$\frac{1}{2}$t,
∵PQ=3-RP=12-t,
∴PN=12-t,
由△PNK∽△DEA可得,NK=6-$\frac{t}{2}$,
∵BM=BC-QC-QM=12-t,
∴又△FBM∽△ECB可得,FM=3-$\frac{t}{4}$,
∴KF=3-$\frac{t}{4}$,
∴S=$\frac{[(3-\frac{t}{4})+(6-\frac{t}{2})]×(12-t)}{2}$=$\frac{3}{8}{t}^{2}-9t+54$(9<t≤12);
综上所述,S=$\left\{\begin{array}{l}{\frac{1}{8}{t}^{2}-\frac{3}{2}t+\frac{9}{2}(0<t≤3)}\\{\frac{3}{4}t-\frac{9}{8}(3<t≤6)}\\{-\frac{1}{4}{t}^{2}+\frac{15}{4}t-\frac{81}{8}(6<t≤9)}\\{\frac{3}{8}{t}^{2}-9t+54(9<t≤12)}\end{array}\right.$;
(3)存在.
理由:过P1作P1S⊥AC于S,P1R⊥DE于R,
∵∠P1QS=60°,P1Q=3,
∴P1S=RE=$\frac{3}{2}\sqrt{3}$,QS=$\frac{3}{2}$,
∴P1R=SE=$\frac{3}{2}$.
①当∠P1GH=90°时,如图: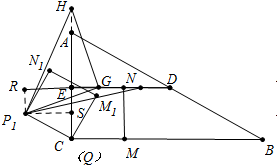
可证△P1RG≌△GEH,
则EG=P1R=$\frac{3}{2}$;
如图: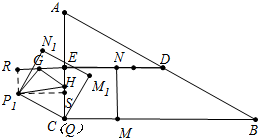
同理可得EG=P1R=$\frac{3}{2}$.
②当∠P1HG=90°时,如图: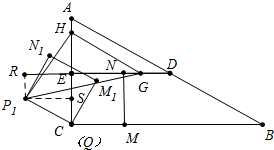
可证△P1SH≌△HEG,
∴EH=P1S=$\frac{3}{2}\sqrt{3}$,EG=SH,
∴EG=EH+SE=$\frac{3}{2}\sqrt{3}+\frac{3}{2}$,
或如图: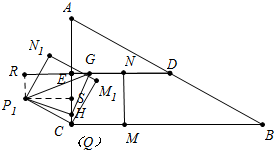
EG=EH-SE=$\frac{3}{2}\sqrt{3}-\frac{3}{2}$;
③当∠GP1H=90°时,
∵P1S≠P1R,∴△P1SH与△P1RG不可能全等.
∴P1H≠P1G,∴不成立.
综上所述,EG的长为$\frac{3}{2}$或$\frac{3}{2}\sqrt{3}+\frac{3}{2}$或$\frac{3}{2}\sqrt{3}-\frac{3}{2}$.
点评 本题以旋转为背景,主要考查了相似形的综合应用、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、平行线的性质等知识,难度较大.解题的关键是根据题意正确画出图形,并学会利用分割法求面积.此外要注意分类讨论思想在解题中的运用,分类时做到不重复,不遗漏.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
已知如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com