
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,
上的点,![]() 且
且![]() 与
与![]() 之间的距离为4,则
之间的距离为4,则![]() 的长为( )
的长为( )

A. 3B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
过点D作DG⊥BE,垂足为G,则GD=4=AB,∠G=90°,再利用AAS证明△AEB≌△GED,根据全等三角形的性质可得AE=EG. 设AE=EG=x,则ED=5﹣x,在Rt△DEG中,由勾股定理得可得方程x2+42=(5﹣x)2, 解方程求得x的值即可得AE的长.
过点D作DG⊥BE,垂足为G,如图所示:

则GD=4=AB,∠G=90°,
∵四边形ABCD是矩形,
∴AD=BC=5,∠A=90°=∠G,
在△AEB和△GED中,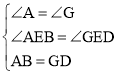
∴△AEB≌△GED(AAS).
∴AE=EG.
设AE=EG=x,则ED=5﹣x,
在Rt△DEG中,由勾股定理得:ED2=EG2+GD2,
∴x2+42=(5﹣x)2,
解得:x=![]() ,即AE=
,即AE=![]() .
.
故选D.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】“囧”(jiǒng)是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为![]() 的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为
的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为![]() 、
、![]() ,剪去的两个小直角三角形的两直角边长也分别为
,剪去的两个小直角三角形的两直角边长也分别为![]() 、
、![]() .
.

(1)用含有![]() 、
、![]() 的式子表示图中“囧”(阴影部分)的面积;
的式子表示图中“囧”(阴影部分)的面积;
(2)当![]() ,
,![]() 时,求此时“囧”(阴影部分)的面积.
时,求此时“囧”(阴影部分)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两汽车从A市出发,丙汽车从B市出发,甲车每小时行驶40千米,乙车每小时行驶45千米,丙车每小时行驶50千米,如果三辆汽车同时相向而行,丙车遇到乙车后10分钟才能遇到甲车,问何时甲丙两车相距15千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形![]() 的顶点
的顶点![]() 同时沿正方形的边开始移动,甲按顺时针方向环行,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第1次相遇在边
同时沿正方形的边开始移动,甲按顺时针方向环行,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第1次相遇在边![]() 上.
上.

(1)它们第2次相遇在边__________上;
(2)它们第2019次相遇在边__________上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(1)填写下表;
层数 | 1 | 2 | 3 | 4 | 5 | … |
该层对应的点数 | 1 | 6 | __________ | __________ | __________ | … |
(2)写出第![]() 层所对应的点数;
层所对应的点数;
(3)是否存在![]() ,使得第
,使得第![]() 层有96个点?如果存在,求出
层有96个点?如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副含30°和45°角的三角尺放置在直线![]() 上.
上.

(1)将图1中的三角尺![]() 绕点
绕点![]() 顺时针方向旋转至如图2所示的位置,
顺时针方向旋转至如图2所示的位置,![]() 在射线
在射线![]() 上,此时
上,此时![]() 旋转的角度为度;
旋转的角度为度;
(2)将图2中的三角尺![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ).
).
①如图3,当![]() 在
在![]() 的内部时,求
的内部时,求![]() 的值;
的值;
②若旋转的速度为每秒15°,经过![]() 秒,当三角尺
秒,当三角尺![]() 与三角尺
与三角尺![]() 的重叠部分以
的重叠部分以![]() 为顶点的角的度数为30°时,求
为顶点的角的度数为30°时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,且∠BAD=80°,则∠DAC的度数是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①垂直于同一直线的两条直线互相平行;②两个无理数的和是无理数;③点![]() 一定不在第四象限;④平方根等于本身的数是
一定不在第四象限;④平方根等于本身的数是![]() 或
或![]() ;⑤若点
;⑤若点![]() 的坐标满足
的坐标满足![]() ,则点
,则点![]() 落在原点上;⑥如果两个角的角平分线互为反向延长线,则这两个角为对顶角.正确个数是( )
落在原点上;⑥如果两个角的角平分线互为反向延长线,则这两个角为对顶角.正确个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com