
 如图,直线
如图,直线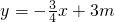 与x、y轴分别交于点A、B,以AB为直径的⊙M过原点O,垂直于x轴的直线MP与⊙M的下半圆交于点P.
与x、y轴分别交于点A、B,以AB为直径的⊙M过原点O,垂直于x轴的直线MP与⊙M的下半圆交于点P. x+3m=0,
x+3m=0,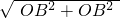 =15,
=15,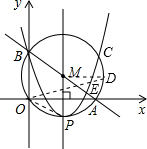
 ,
, ),
),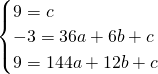 ,
, .
. x2-4x+9;
x2-4x+9; ),MD=
),MD= AB=
AB= ,
, ,
, )
) ,
, )代入解得k=
)代入解得k= ,
, x,
x,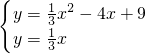 ,
,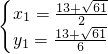 或
或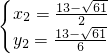 ,
,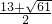 ,
,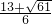 ),(
),(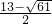 ,
,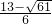 ).
).

科目:初中数学 来源:2012届浙江省四校九年级联考数学卷(带解析) 题型:填空题
如图:直线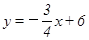 与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值: ▲ .
与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值: ▲ .
查看答案和解析>>
科目:初中数学 来源:2004年四川省广安市中考数学试卷(解析版) 题型:解答题
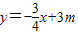 与x、y轴分别交于点A、B,以AB为直径的⊙M过原点O,垂直于x轴的直线MP与⊙M的下半圆交于点P.
与x、y轴分别交于点A、B,以AB为直径的⊙M过原点O,垂直于x轴的直线MP与⊙M的下半圆交于点P.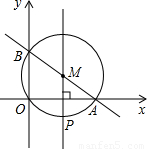
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省金四校九年级联考数学卷(解析版) 题型:填空题
如图:直线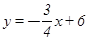 与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值: ▲ .
与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值: ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线
如图,直线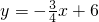 与x,y轴分别交于点A,C,过点A、C分别作x,y轴的垂线,交于点B,点D为AB的中点.点P从点A出发,以每秒1个单位的速度,沿△AOC边 A→O→C→A的方向运动,运动时间为t(秒).
与x,y轴分别交于点A,C,过点A、C分别作x,y轴的垂线,交于点B,点D为AB的中点.点P从点A出发,以每秒1个单位的速度,沿△AOC边 A→O→C→A的方向运动,运动时间为t(秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com