练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图，BO平分∠ABC，CO平分∠ACB，且MN∥BC，设AB=12，BC=24，AC=10，则△AMN的周长为（　　）
    A．22B．36C．46D．34

    分析 根据BO平分∠ABC，CO平分∠ACB，且MN∥BC，可得出MO=MC，NO=NB，所以三角形AMN的周长是AB+AC．

    解答 解：∵BO平分∠CBA，CO平分∠ACB，
    ∴∠MBO=∠OBC，∠OCN=∠OCB，
    ∵MN∥BC，
    ∴∠MOB=∠OBC，∠NOC=∠OCB，
    ∴∠MBO=∠MOB，∠NOC=∠NCO，
    ∴MO=MB，NO=NC，
    ∵AB=12，AC=18，
    ∴△AMN的周长=AM+MN+AN=AB+AC=12+10=22．
    故选A．

    点评 本题主要考查学生对考查了等腰三角形的判定和性质以及平行线的性质等知识点的理解和掌握，难度不大，是基础知识要熟练掌握．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．已知关于x的方程x2+（2m-1）x+m2+2=0的两根为x1，x2，且两根的积是两根和的2倍．
    （1）求m的值；
    （2）求|x1-x2|的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．对平面直角坐标系中的点P（x，y），定义d=|x|+|y|，我们称d为P（x，y）的幸福指数．对于函数图象上任意一点P（x，y），若它的幸福指数d≥1恒成立，则称此函数为幸福函数，如二次函数y=x2+1就是一个幸福函数，理由如下：设P（x，y）为y=x2+1上任意一点，d=|x|+|y|=|x|+|x2+1|，∵|x|≥0，|x2+1|=x2+1≥1，∴d≥1．∴y=x2+1是一个幸福函数．
    （1）若点P在反比例函数y=$\frac{1}{x}$的图象上，且它的幸福指数d=2，请直接写出所有满足条件的P点坐标；
    （2）一次函数y=-x+1是幸福函数吗？请判断并说明理由；
    （3）若二次函数y=x2-（2m+1）x+m2+m（m＞0）是幸福函数，试求出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．把八个完全相同的小球平分为两组，每组中每个分别协商1，2，3，4四个数字，然后分别装入不透明的口袋内搅匀，从第一个口袋内取出一个数记下数字后作为点P的横坐标x，然后再从第二个口袋中取出一个球记下数字后作为点P的纵坐标，则点P（x，y）落在直线y=-x+5上的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{4}$C．$\frac{1}{3}$D．$\frac{1}{6}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．先化简，再求值：
    （1+$\frac{1}{x-1}$）÷$\frac{1}{{x}^{2}-1}$-（x-2），然后从$\sqrt{2}$，1，-1中选取一个你认为合适的数作为x的值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解不等式组：$\left\{{\begin{array}{l}\frac{x}{2}+4≤1\\ x-8＞2（x+2）.\end{array}}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

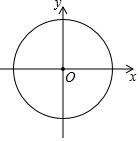    12．在平面直角坐标系xOy中，⊙O的半径是5，点A为⊙O上一点，AB⊥x轴于点B，AC⊥y轴于点C，若四边形ABOC的面积为12，写出一个符合条件的点A的坐标（3，4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

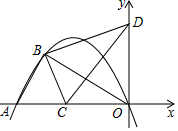    9．如图，抛物线y=$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$与x轴交于点A和原点O，点B（-8，n）在抛物线上，连接AB、OB．
    （1）n=4，OA=10；
    （2）点C（m，0）在线段OA上运动（不与A、O重合），BD⊥BC，交y轴正半轴于点D，求△BCD的面积S与m的函数关系式，并求S的最小值；
    （3）在（2）的条件下，是否存在△OCD与△OAB相似？若存在．请直按写出m的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．表是抄录百联海上国际影城票务网公布的三个电影的票价，如图是按照某学校购买的200张门票的种类、数量绘制的扇形图：
    电影票价（元/张）
    《少年派》80
    《十二生肖》70
    《大上海》90
    依据上列图表，回答下列问题：
    （1）购买电影《大上海》的电影票数量占全部电影票数量的20%；
    （2）图中表示《大上海》电影票数量的扇形的圆心角是72度；
    （3）购买电影《十二生肖》的电影票数量是100张；
    （4）购买电影《少年派》的总票价占全部电影票总票价的$\frac{24}{77}$（填几分之几）．

    查看答案和解析>>

    同步练习册答案