
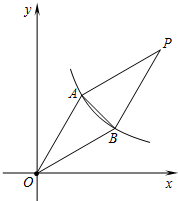
 已知:如图,双曲线y=$\frac{k}{x}$在第一象限的分支经过A、B两点,点A的坐标为(2,2$\sqrt{3}$),点B的坐标为(m,2).
已知:如图,双曲线y=$\frac{k}{x}$在第一象限的分支经过A、B两点,点A的坐标为(2,2$\sqrt{3}$),点B的坐标为(m,2).分析 (1)把A点坐标代入反比例函数解析式可求得k,把B点坐标代入反比例函数解析式则可求得m;
(2)过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,由A、B两点的坐标可分别求得OC、AC、OB、OD,利用三角函数的定义可分别求得∠AOC和∠BOD,可求得∠AOB的度数;
(3)连接OP交AB于点H,分别过点H、P作HE⊥E轴、PF⊥E轴,由条件可知四边形OAPB为菱形,可证得H为AB、OP的中点,E为CD的中点,则EH为△OFP的中位线,借助(2)中OC、OD可求得OE,且可得到△HOE和△POF为等腰直角三角形,可求得PF和OF的长,从而可求得P点坐标.ω
解答 解:
(1)把A点的坐标 (2,$2\sqrt{3}$)代入y=$\frac{k}{x}$,可得k=4$\sqrt{3}$,
∴反比例函数解析式为y=$\frac{4\sqrt{3}}{x}$,
把B点的坐标 (m,2)代入y=$\frac{4\sqrt{3}}{x}$,可得m=2$\sqrt{3}$;
(2)如图1,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,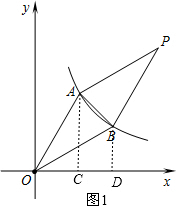
∵A点的坐标 (2,2$\sqrt{3}$),
∴OC=2,AC=2$\sqrt{3}$,
∴tan∠AOC=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠AOC=60°,
∵B点的坐标 (2$\sqrt{3}$,2),
∴OD=2$\sqrt{3}$,BD=2,
∴tan∠BOD=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠BOD=30°,
∴∠AOB=∠AOC-∠BOD=30°;
(3)如图2,连接OP交AB于点H,分别过点H、P作HE⊥E轴、PF⊥E轴,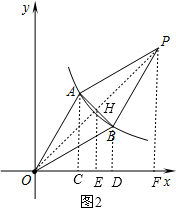
∵A(2,2$\sqrt{3}$),B(2$\sqrt{3}$,2)
∴OC=2,OD=2$\sqrt{3}$,
∴CD=OD-OC=2$\sqrt{3}$-2,
∵△AOB沿AB翻折,
∴四边形OBPA为菱形,
∴∠HOB=$\frac{1}{2}$∠AOB=15°,HA=HB,HO=HP
∴∠HOE=45°,
∴△OEH为等腰直角三角形,
∵AC⊥x轴、HE⊥x轴、BD⊥x轴,
∴AC∥BD∥HE,
∴E为CD中点,
∴OE=HE=OC+CE=OC+$\frac{1}{2}$CD=2+$\frac{1}{2}$(2$\sqrt{3}$-2)=$\sqrt{3}$+1,
∵HO=HP,HE∥PF,
∴HE为△OPF的中位线,
∴PF=2HE,
∴PF=2($\sqrt{3}$+1),
∴OF=PF=2($\sqrt{3}$+1)=2$\sqrt{3}$+2,
∴P点坐标为(2$\sqrt{3}$+2,2$\sqrt{3}$+2).
点评 本题为反比例函数的综合应用,涉及知识点有待定系数法、三角函数的定义、菱形的判定和性质、等腰直角三角形的判定和性质、中位线定理等.在(2)中根据点的坐标求得相应线段的长是解题的关键,在(3)中利用好中位线定理的判定和性质是解题的关键.本题考查知识点较多,综合性很强,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
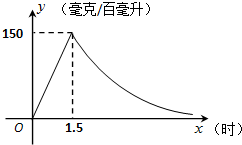 实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:
实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )
已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )| A. | (5,8) | B. | (5,10) | C. | (4,8) | D. | (3,10) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点B,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点A,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的同侧,AB=4,CD=3,AB与CD的距离为1,则a-b的值是12.
如图,已知点B,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点A,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的同侧,AB=4,CD=3,AB与CD的距离为1,则a-b的值是12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m$>\frac{1}{3}$ | B. | m$<\frac{1}{3}$ | C. | m$≥\frac{1}{3}$ | D. | m$≤\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
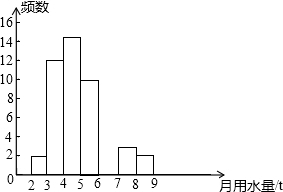 小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 15 | 30% |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com