
【题目】解方程
(1)(x﹣5)2=16(直接开平方法) (2)x2﹣4x+1=0(配方法)
(3)x2+3x﹣4=0(公式法) (4)x2+5x﹣3=0(配方法)
【答案】(1)x1=9,x2=1;(2)x1=2+![]() ,x2=2﹣
,x2=2﹣![]() ;(3)x1=1,x2=﹣4;(4)x1=
;(3)x1=1,x2=﹣4;(4)x1=![]() ,x2=
,x2=![]() .
.
【解析】试题分析:(1)按要求利用直接开平方法进行求解即可;
(2)按要求利用配方法根据配方法的步骤进行求解即可;
(3)按要求利用公式法进行求解即可;
(4)按要求利用配方法根据配方法的步骤进行求解即可.
试题解析:(1)(x﹣5)2=16,
x-5=±4,
x-5=4或x-5=-4,
∴x1=9,x2=1;
(2)x2﹣4x+1=0,
x2﹣4x=-1,
x2﹣4x+4=-1+4,
(x-2)2=3,
x-2=±![]() ,
,
∴x1=2+![]() ,x2=2﹣
,x2=2﹣![]() ;
;
(3)x2+3x﹣4=0,
a=1,b=3,c=-4,
b2-4ac=32-4×1×(-4)=25>0,
![]() ,
,
∴x1=1,x2=﹣4;
(4)x2+5x﹣3=0,
x2+5x=3,
x2+5x+![]() =3+
=3+![]() ,
,
![]() ,
,
![]() ,
,
∴x1=![]() ,x2=
,x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列方程变形中,正确的是( )
A.方程3x-2=2x+1,移项,得3x-2x=1-2
B.方程3-x=2-5(x-1),去括号,得3-x=2-5x-1;
C.方程-75x=76,方程两边同除以-75,得x=-![]()
D.方程![]() =1+
=1+![]() ,去分母,得2(2x-1)=6+3(x-3)
,去分母,得2(2x-1)=6+3(x-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,则下面的结论:①
,则下面的结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论有( )
,其中正确结论有( )
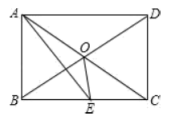
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若有a,b两个数,满足关系式:a+b=ab﹣1,则称a,b为“共生数对”,记作(a,b).
例如:当2,3满足2+3=2×3﹣1时,则(2,3)是“共生数对”.
(1)若(x,﹣2)是“共生数对”,求x的值;
(2)若(m,n)是“共生数对”,判断(n,m)是否也是“共生数对”,请通过计算说明.
(3)请再写出两个不同的“共生数对”
查看答案和解析>>
科目:初中数学 来源: 题型:
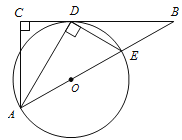
【题目】已知:如图,在△ABC 中,∠C=90°,∠BAC 的平分线 AD 交 BC于点 D,过点 D 作 DE⊥AD 交 AB 于点 E,以 AE 为直径作⊙O.
(1)求证:BC 是⊙O 的切线;
(2)若 AC=3,BC=4,求 BE 的长.
(3)在(2)的条件中,求 cos∠EAD 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
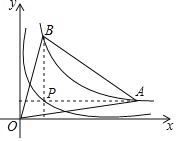
【题目】如图,点P为函数y=![]() (x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y
(x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y![]() (x>0)的图象交于点A,B,则△AOB的面积为_____.
(x>0)的图象交于点A,B,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y=ax+b的图象交于点A(1,4)和点B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得![]() >ax+b成立的自变量x的取值范围;
>ax+b成立的自变量x的取值范围;
(3)过点A作AC⊥x轴,垂足为C,在平面内有点D,使得以A,O,C,D四点为顶点的四边形为平行四边形,直接写出符合条件的所有D点的坐标.
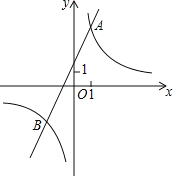
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,市民积极参与义务植树活动,小刚同学为了了解自己小区300户家庭在2019年3月义务植树的数量,进行了抽样调查,随机抽取了其中30户家庭,收集的数据如下:(单位:颗)
![]()
(1)对以上数据进行整理、描述和分析
①绘制如下的统计图,请补充完整
②这30户家庭2019年3月份义务植树数量得中位数是 ,众数是 .
(2)“互联网![]() 全民义务植树”是新时代首次全民义务植树组织形式和尽责方式的一大创新,并推出义务植树网上预约服务,小刚同学所调查的这30户家庭有7户家庭采用的网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有多少户?
全民义务植树”是新时代首次全民义务植树组织形式和尽责方式的一大创新,并推出义务植树网上预约服务,小刚同学所调查的这30户家庭有7户家庭采用的网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建足球特色学校,营造足球文化氛围,某学校随机抽取部分八年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分—10分,B级:7分—7.9分,C级:6分—6.9分,D级:1分—5.9分)根据所给信息,解答以下问题:
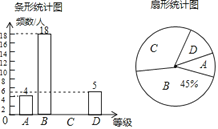
(1)样本容量为 ,C对应的扇形的圆心角是____度,补全条形统计图;
(2)所抽取学生的足球运球测试成绩的中位数会落在____等级;
(3)该校八年级有300名学生,请估计足球运球测试成绩达到![]() 级的学生有多少人?
级的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com