
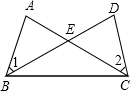
 已知:如图,AB=DC,∠1=∠2.求证:∠EBC=∠ECB.
已知:如图,AB=DC,∠1=∠2.求证:∠EBC=∠ECB.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
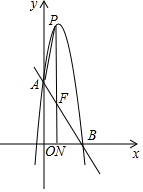 如图,直线y=-$\frac{3}{2}$x+3分别交y轴、x轴于点A,B,抛物线y=-4x2+bx+c经过点A,B,点P在该抛物线的图象上,作PN⊥x轴于点N,PN交射线AB于点F,连结AP,设点P横坐标为n(n>0).
如图,直线y=-$\frac{3}{2}$x+3分别交y轴、x轴于点A,B,抛物线y=-4x2+bx+c经过点A,B,点P在该抛物线的图象上,作PN⊥x轴于点N,PN交射线AB于点F,连结AP,设点P横坐标为n(n>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
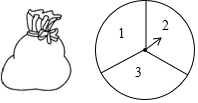 一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
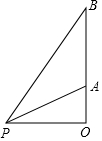 如图,一枚火箭从地面O处发射,在距离发射点9km处的地面观测站P点测得火箭底部到达A点时,其底部的仰角为30°;20s后火箭底部到达B点,测得其底部的仰角为60°.求这枚火箭从A点到B点的平均速度(精确到 0.1km/s)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)
如图,一枚火箭从地面O处发射,在距离发射点9km处的地面观测站P点测得火箭底部到达A点时,其底部的仰角为30°;20s后火箭底部到达B点,测得其底部的仰角为60°.求这枚火箭从A点到B点的平均速度(精确到 0.1km/s)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com