
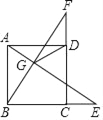
【题目】如图,在正方形ABCD中,BC=2,E、F分别为射线BC,CD上两个动点,且满足BE=CF,设AE,BF交于点G,连接DG,则DG的最小值为_______.
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把直角三角形纸片沿过顶点B的直线(BE交CA于E)折叠,直角顶点C落在斜边AB上,如果折叠后得等腰△EBA,那么结论中:①∠A=30°;②点C与AB的中点重合;③点E到AB的距离等于CE的长,正确的个数是( )
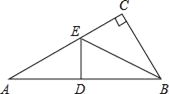
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级学生在学习等腰三角形的相关知识时时,经历了以下学习过程:
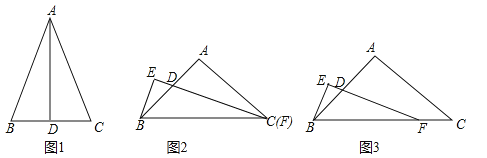
(1)(探究发现)如图1,在![]() 中,若
中,若![]() 平分
平分![]() ,
,![]() 时,可以得出
时,可以得出![]() ,
,![]() 为
为![]() 中点,请用所学知识证明此结论.
中点,请用所学知识证明此结论.
(2)(学以致用)如果![]() 和等腰
和等腰![]() 有一个公共的顶点
有一个公共的顶点![]() ,如图2,若顶点
,如图2,若顶点![]() 与顶点
与顶点![]() 也重合,且
也重合,且![]() ,试探究线段
,试探究线段![]() 和
和![]() 的数量关系,并证明.
的数量关系,并证明.
(3)(拓展应用)如图3,在(2)的前提下,若顶点![]() 与顶点
与顶点![]() 不重合,
不重合,![]() ,(2)中的结论还成立吗?证明你的结论
,(2)中的结论还成立吗?证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要使得△ABC是等腰三角形,则需要满足下列条件中的( )
A. ∠A=50°,∠B=60° B. ∠A=50°,∠B=100° C. ∠A+∠B=90° D. ∠A+![]() ∠B=90°
∠B=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 各有一个角是![]() 的两个等腰三角形相似 B. 各有一个角是
的两个等腰三角形相似 B. 各有一个角是![]() 的两个等腰三角形相似
的两个等腰三角形相似
C. 有两边对应成比例的两个等腰三角形相似 D. 两腰对应成比例的两个等腰三角形相似
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com