
【题目】如图①,在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.
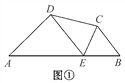
【试题再现】如图②,在△ABC中,∠ACB=90°,直角顶点C在直线DE上,分别过点A,B作AD⊥DE于点D,BE⊥DE于点E.求证:△ADC∽△CEB.
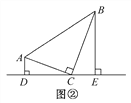
【问题探究】在图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由.
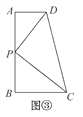
【深入探究】如图③,AD∥BC,DP平分∠ADC,CP平分∠BCD交DP于点P,过点P作AB⊥AD于点A,交BC于点B.
(1)请证明点P是四边形ABCD的边AB上的一个强相似点.
(2)若AD=3,BC=5,试求AB的长.
【答案】【试题再现】见解析;【问题探究】点E是四边形ABCD的边AB上的相似点. 理由见解析;【深入探究】(1) 点P是四边形ABCD的边AB上的一个强相似点,见解析;(2) ![]()
【解析】试题分析:【试题再现】易证∠BCE=∠CAD,又∠ADC=∠CEB=90°,故得△ADC∽△CEB.
【问题探究】要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解.
【深入探究】(1)分别证明△ADP∽△PDC,△BPC∽△PDC,从而△ADP∽△PDC∽△BPC,故点P是四边形ABCD的边AB上的一个强相似点.
(2)过点P作PE⊥DC于点E,过点D作DF⊥BC于点F,则四边形ABFD是矩形,通过证明△ADP≌△EDP和△CBP≌△CEP得DC =8,再求出CF=2,在Rt△CDF中,由勾股定理,得AB=2![]() .
.
试题解析:【试题再现】
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,
∴∠ACD+∠CAD=90°,
∴∠BCE=∠CAD,
∵∠ADC=∠CEB=90°,
∴△ADC∽△CEB.
【问题探究】点E是四边形ABCD的边AB上的相似点.
理由如下:
∵∠DEC=40°,
∴∠DEA+∠CEB=140°.
∵∠A=40°,
∴∠ADE+∠AED=140°,
∴∠ADE=∠CEB,
又∵∠A=∠B,
∴△ADE∽△BEC,
∴点E是四边形ABCD的边AB上的相似点.
【深入探究】
(1)∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DP平分∠ADC,CP平分∠BCD,
∴∠CDP+∠DCP=![]() (∠ADC+∠BCD)=90°,
(∠ADC+∠BCD)=90°,
∵DA⊥AB,DA∥BC,
∴CB⊥AB,
∴∠DPC=∠A=∠B=90°,
∵∠ADP=∠CDP,
∴△ADP∽△PDC,同理△BPC∽△PDC,
∴△ADP∽△PDC∽△BPC,即点P是四边形ABCD的边AB上的一个强相似点.
(2)过点P作PE⊥DC于点E,过点D作DF⊥BC于点F,则四边形ABFD是矩形,
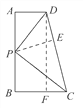
∴DF=AB,
在△ADP与△EDP中,
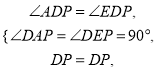
∴△ADP≌△EDP,
∴AD=DE,
同理△CBP≌△CEP,∴BC=EC,
∴DC=AD+BC=8.
在Rt△CDF中,CF=BC-BF=BC-AD=5-3=2,
由勾股定理,得DF=![]() =2
=2![]() ,
,
∴AB=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知如图:点(1,3)在函数y=![]() (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某造纸企业为了更好地处理污水问题,决定购买10台新型污水处理设备.甲、乙两种型号的设备可选,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/) | 10 | 8 |
处理污水量(吨/月) | 180 | 150 |
(1)经预算:该企业购买污水处理设备的资金不超过85万元,你认为该企业有哪几种购买方案.
(2)在(1)的条件下,若每月需要处理的污水不低于1530吨,为了节约资金,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如果一个正整数能表示为两个连续奇数的平方差,那么我们称这个正整数为“和谐数”,如8=32-12,16=52-32,24=72-52,因此,8,16,24这三个数都是“和谐数”.
(1)在32,75,80这三个数中,是和谐数的是______;
(2)若200为和谐数,即200可以写成两个连续奇数的平方差,则这两个连续奇数的和为______;
(3)小鑫通过观察发现以上求出的“和谐数”均为8的倍数,设两个连续奇数为2n-1和2n+1(其中n取正整数),请你通过运算验证“和谐数是8的倍数”这个结论是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() .
.
(1)a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值与a的取值无关,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师为了了解班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查.他将调查结果分为四类:A:很好;B:较好;C:一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)请计算出A类男生和C类女生的人数,并将条形统计图补充完整.
(2)为了共同进步,张老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com